前几天,小灰发布了
漫画中有几个细节问题,这一次小灰做了全面修改。
修改问题如下:
1.合并后数组左半部分和右半部分的关系是“小于等于”,而不是原文中所说的“小于”
2.原文对边界条件的说明有误。当数组A所有元素都小于数组B时,j的值并不会等于0。
在此感谢小伙伴们的细心指正。


————— 第二天 —————



什么意思呢?让我们来看两个例子:
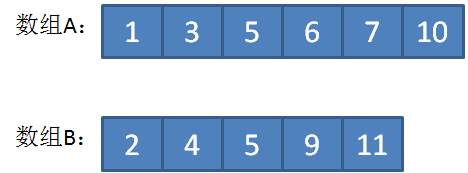
上图这两个给定数组A和B,一个长度是6,一个长度是5,归并之后的大数组仍然要保持升序,结果如下:
大数组的长度是奇数(11),中位数显然是位于正中的第6个元素,也就是元素5。
上面的例子是奇数个元素的情况。那么偶数的元素是什么样呢?让我们来看另一个例子:
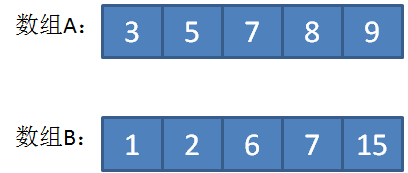
上图这两个给定数组A和B,长度都是5,归并之后的大数组如下:

大数组的长度是偶数(10),位于正中的元素有两个,分别是6和7,这时候的中位数就是两个数的平均值,也就是6.5。






————————————






或许这听起来有点绕,我们仍然用刚才的例子来说明:
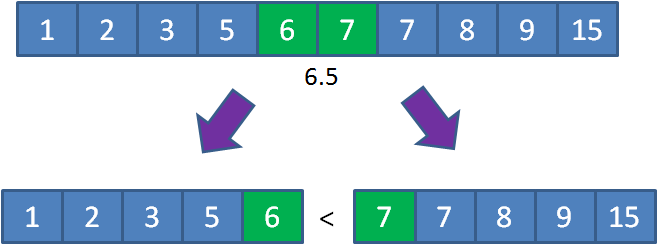
如上图所示,对于偶数长度的数组,可以根据中位数分成长度相等的两部分,左半部分最大元素(6),永远小于等于右半部分的最小元素(7)。
对于奇数长度的数组,同样可以根据中位数分成两部分:
如上图所示,对于奇数长度的数组,如果把中位数本身归入左半部分,则左半边长度= 右半边长度+1。
左半部分最大元素(5),永远小于等于右半部分的最小元素(6)。


什么意思呢?大数组被中位数等分的左右两部分,每一部分根据来源又可以再划分成两部分,其中一部分来自数组A的元素,另一部分来自数组B的元素:
如图所示,原始数组A和B,各自分成绿色和橙色两部分。其中数值较小的绿色元素组成了大数组的左半部分,数值较大的橙色元素组成了大数组的右半部分。
最重要的是,绿色元素和橙色元素的数量是相等的(偶数情况),而且最大的绿色元素小于等于最小的橙色元素。
假设数组A的长度是m,绿色和橙色元素的分界点是i,数组B的长度是n,绿色和橙色元素的分界点是j,那么为了让大数组的左右两部分长度相等,则i和j需要符合如下两个条件:
i + j=(m+n+1)/2
(之所以m+n后面要再加1,是为了应对大数组长度为奇数的情况)
Max(A[i-1],B[j-1]) = B[0]且B[1]>=A[4],所以这一组i和j是合适的!
第七步,找出中位数
如果大数组长度是奇数,那么:
中位数 =Max(A[i-1],B[j-1])
(也就是大数组左半部分的最大值)
如果大数组长度是偶数,那么:
中位数 = (Max(A[i-1],B[j-1]) + Min(A[i], B[i]))/2
(也就是大数组左半部分的最大值和大数组右半部分的最小值取平均)
在本例中,大数组长度是奇数,所以中位数=Max(8,1) = 8


1.数组A的长度远大于数组B
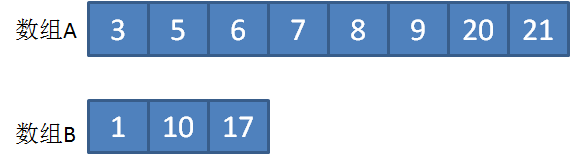
也就是m远大于n,这时候会出现什么问题呢?
当我们设定了i的初值,也就是数组A正中间的元素,再计算j的时候有可能发生数组越界。
因此,我们可以提前把数组A和B进行交换,较短的数组放在前面,i从较短的数组中取。
这样做还有一个好处,由于数组A是较短数组,i的搜索次数减少了。
2.无法找到合适的i值
什么情况下会无法找到合适的i值呢?有两种情况:
数组A的长度小于数组B,并且数组A的所有元素都大于数组B。
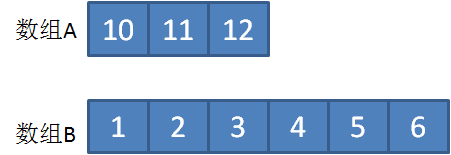
这种情况下,无法通过二分查找寻找到符合B[j−1]≤A[i]&& A[i−1]≤B[j]的i值,一直到i=0为止。
此时我们可以跳出二分查找的循环,所求的中位数是B[j-1]。(仅奇数情况)
数组A的长度小于数组B,并且数组A的所有元素都小于数组B。
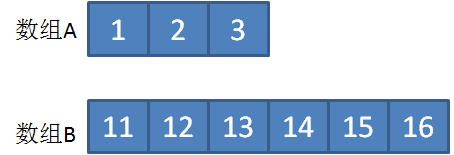
这种情况下,同样无法通过二分查找寻找到符合B[j−1]≤A[i]&& A[i−1]≤B[j]的i值,一直到i=(数组A长度-1)为止。
此时我们可以跳出二分查找的循环,所求的中位数是Max(A[i-1],B[j-1])。(仅奇数情况)

public static double findMedianSortedArrays(int[] arrayA, int[] arrayB) {
int m = arrayA.length;
int n = arrayB.length;
//如果数组A的长度大于等于数组B,则交换数组
if (m > n) {
int[] temp = arrayA;
arrayA = arrayB;
arrayB = temp;
int tmp = m;
m = n;
n = tmp;
}
int start = 0;
int end = m;
int mid = (m + n + 1) / 2;
while (start <= end) {
int i = (start + end) / 2;
int j = mid - i;
if (i < end && arrayB[j-1] > arrayA[i]){
//i偏小了,需要右移
start = i + 1;
}
else if (i > start && arrayA[i-1] > arrayB[j]) {
//i偏大了,需要左移
end = i - 1;
}
else {
//i刚好合适,或i已达到数组边界
int maxLeft;
if (i == 0) {
maxLeft = arrayB[j-1];
} else if (j == 0) {
maxLeft = arrayA[i-1];
} else {
maxLeft = Math.max(arrayA[i-1], arrayB[j-1]);
}
if ( (m + n) % 2 == 1 ) {
//如果大数组的长度是奇数,中位数就是左半部分的最大值
return maxLeft;
}
int minRight;
if (i == m) {
minRight = arrayB[j];
} else if (j == n) {
minRight = arrayA[i];
} else {
minRight = Math.min(arrayB[j], arrayA[i]);
}
//如果大数组的长度是偶数,取左侧最大值和右侧最小值的平均
return (maxLeft + minRight) / 2.0;
}
}
return 0.0;
}
public static void main(String[] args) {
int[] arrayB = new int[]{3,5,6,7,8,12,20};
int[] arrayA = new int[]{1,10,17,18};
System.out.println(findMedianSortedArrays(arrayA, arrayB));
}




—————END—————
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777