两个数组-寻找两个正序数组的中位数

题目:

给定两个大小分别为m和n的正序（从小到大）数组nums1和nums2。请你找出并返回这两个正序数组的中位数。

算法的时间复杂度应该为O(log (m+n))。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

分析:

寻找两个数组的中位数，也就是将两个数组进行合并再求其中位数是等效的，但是题目要求并没有合并，而是根据两个数据进行求中位数，那么就需要分析一下，中位数指的是将一组数据按照从小到大的顺序排列后，处于中间位置的数值，而中位数分为偶数情况和奇数情况,分为下面的几种，我们分别说一下其情况

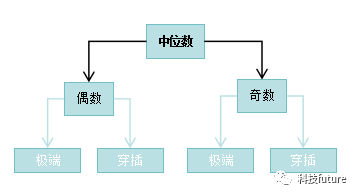
数组词多音字_数组的定义_两个数组

说明一下，偶数/奇数极端情况就是两个数组中，一个数组全是很小的数，另一个数组全是很大的数，并且一个数组的所有元素都大于另一个数组的所有元素，偶数/奇数穿插就是两个数组大小随机并不是极端情况。

偶数穿插情况:

偶数穿插情况就是第一数组和第二个数组中的元素按照从小到大排序的时候中位数的边界绘制一条分界线，这条分界线的左侧和右侧元素正好相同，那么中位数的值就是左侧蓝色部分两个元素的最大值和右侧绿色的部分的最小值的平均值。那么我们不妨就考虑左侧的边界，会发现一个有趣的规律，左侧的两个元素的序数相加等于两个数组长度之和的一半，即(i+j)=(m+n)/2

i+j = (m+n)/2 % 分界线左侧的i和j

偶数极端情况:

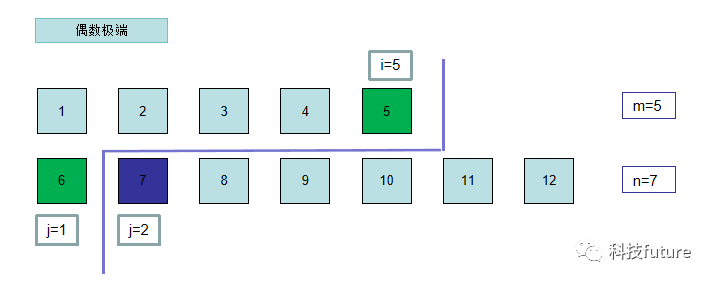
两个数组_数组词多音字_数组的定义

当偶数极端情况下，中位数分界线左侧中绿色元素的最大值和分界线右侧的最小值的和的平均值，此情况中边界在第一个数组的终点，那么右侧只有一个元素是最小值，而上述的偶数穿插中，右侧有两个元素其中一个是最小值，其中会发现分界线左侧的两个数组的边界元素序数之和等于两个数组长度之和的一半，即i+j=(m+n)/2,

i+j = (m+n)/2

奇数极端情况:

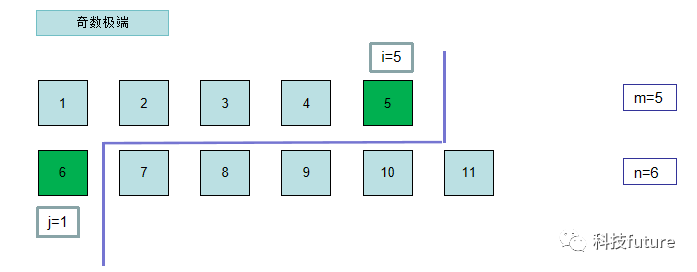
数组词多音字_数组的定义_两个数组

在偶数情况中，两边的元素在分界线下都是相等的，而奇数情况，在分界线下，分界线的左右是相差一个元素的，当分界线的左边多于右边1个元素的时候，中位数就是左侧的最大值，这是只说明第一个数组短于第二个数组的情况，其他情况可以进行转换为上图的情况。而其边界值和数组长度依旧有些规律，i+j = (m+n+1)/2

i+j = (m+n+1)/2

奇数穿插情况:

而到了奇数穿插的情况，因为边界是四个元素，上图中相同颜色是分界线的同侧，所以当左侧元素的数量大于右侧的数量的时候，中位数就是左侧元素边界中的最大值。我们依旧可以找到数值上的规律i+j=(m+n+1)/2

从上述中我们可以发现规律，边界一侧的两个元素的序数和数组长度的关系为i+j=(m+n)/2或者i+j=(m+n+1)/2；我们把公式进行统一使用i+j=(m+n+1)//2

i+j=(m+n+1)//2  % 取整数，无论是偶数还是奇数都能相等

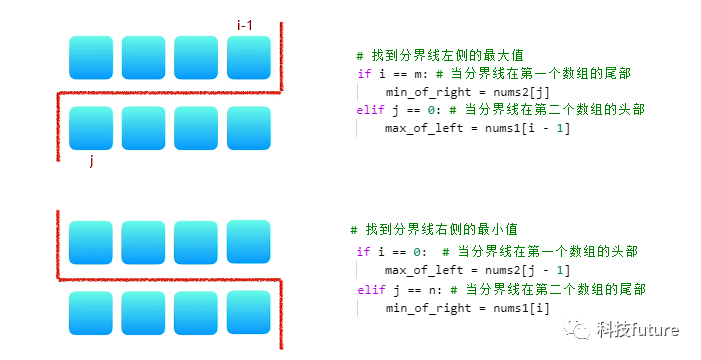
知道了上面的规律，我们下一步就是找边界，因为序列i和j相关联，且m+n是固定值，所以找到较短数组的序列边界i，就可以找到另一个数组的边界j；并且我们还会发现边界上的交叉位置上的值必须是小于等于，如下图所示

数组词多音字_数组的定义_两个数组

二分查找

当然上面要确定边界还需要二分查找方法，其实查找第一个数组的边界就能知道第二个数组的边界，因为知道i对应的j自然就出现，我们如何判断此边界就是我们要找的边界呢?首先如果是我们查找的边界具有如下特征:

通过二分法不断的取区间的中间位置，然后通过边界的特征判断当前的边界是否是我们查找的边界，然后不断的缩小区间范围，直到我们找到我们想要的特征边界为止。

代码:

class Solution:    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:        # 获取两个数组的长度        m, n = len(nums1), len(nums2)        # 如果数组nums1的长度大于nums2的长度，则交换两个数组以确保nums1的长度较小        if m > n:            nums1, nums2, m, n = nums2, nums1, n, m
        # 初始化二分查找的边界,定义最短数组的范围        imin, imax = 0, m        # 两个数组的中位数位置        half_len = (m + n + 1) // 2
        # 使用二分查找找到合适的分割点        while imin <= imax:            # 二分法先初始i的位置            i = (imin + imax) // 2  # 在nums1中进行二分查找的位置            # 通过i+j=(m+n+1)//2的关系确定j            j = half_len - i  # 在nums2中对应的位置
            # 根据分割点进行比较，调整边界            # 注意我们说的第i个元素,那么代码中就是第i-1个            # 右上角小于左下角            if i < m and nums2[j - 1] > nums1[i]: # 此时分界线在前面                # 现在分界线太靠后                imin = i + 1            # 左上角大于右下角            elif i > 0 and nums1[i - 1] > nums2[j]:                # 现在的分界线太靠前                imax = i - 1            # 此时分界线刚刚好            else:                # 找到分界线左侧的最大值                if i == 0:  # 当分界线在第一个数组的头部                    max_of_left = nums2[j - 1]                elif j == 0: # 当分界线在第二个数组的头部                    max_of_left = nums1[i - 1]                # 当边界线在两个数组的中间的最大值                else:                    max_of_left = max(nums1[i - 1], nums2[j - 1])
                if (m + n) % 2 == 1:  # 总元素个数为奇数                    return max_of_left
                # 找到分界线右侧的最小值                if i == m: # 当分界线在第一个数组的尾部                    min_of_right = nums2[j]                elif j == n: # 当分界线在第二个数组的尾部                    min_of_right = nums1[i]                # 当边界线在两个数组的中间的最小值                else:                    min_of_right = min(nums1[i], nums2[j])                # 总元素个数为偶数                return (max_of_left + min_of_right) / 2.0
        return 0.0  # 处理特殊情况，例如某个数组为空数组