Noether was the most significant creative mathematical genius thus far produced since the higher education of women began。 ——Albert Einstein
在提出的次年就获得了诺贝尔奖,杨振宁、李政道等人提出的宇称不守恒彻底摧毁了1956年前物理学家对于对称的完美幻想,且这个发现也持续地影响着后世。虽然作者能力有限,但要想了解宇称不守恒,应该从诺特定理开始。本系列尽可能不包含公式,因为作者也不懂这些。
01
诺特定理

诺特定理,由德国数学家艾米·诺特于20世纪初提出,为理论物理的中心结果之一,表达了连续对称性和守恒定律的一一对应,也就是说每一种不同的对称都对应着一种守恒。今天就来讲讲其中的时间平移对称,空间平移对称,空间旋转对称和镜像对称。
首先讲讲时间平移对称,它的大致意思是我们今天实验做出的结果和明天实验做出的结果是一样的。核心思想是实验结果不会因为时间的变化而变化,而它也和能量守恒定律相对应。举个例子,假如物理规律是可变的,那么假设万有引力常数越变越大,那今天苹果掉到地上的所释放出的能量会小于明天苹果在相同情况下掉到地上所释放的能量,因为万有引力常量越变越大了。这样一来不就凭空造出了能量。

说完了时间平移对称,再来讲讲空间平移对称。再拿苹果举例,空间平移对称的意思是你在上海扔下一个苹果和在北京同一高度扔下一个苹果将释放出同等的能量,其核心思想是物理定律不随着地点变化而改变,而它则对应了动量守恒定律。大致的解释请看下面的高糊图片。

当两个小球碰撞在一起时,它们之间产生的相互作用力拥有方向相反的特性,而根据牛顿第二定律,F=ma,可以得出表达式Δt×F=mΔv。由于相互作用力同时产生同时消失且Δt1和Δt2都为标量,也就是只有大小没有方向的物理量,所以Δt1=Δt2。于是,由于Δt1=Δt2且F1=-F2,两个小球碰撞产生的力方向相反,大小相同。将两者合并后可以得出,一式的动量(Δp)和二式的动量相加等于0,意味着在整个碰撞的过程中动量没有发生改变,即动量守恒。大家还有不懂的地方可以在公众号后台留言,作者会看到且知道答案的话都会进行回答。
ok现在看看第三个对称性,也就是空间旋转对称性。举个例子,你往北方踢一脚足球和往南方踢一脚足球所得出的物理规律是一样的。换个例子说,你在实验室里做实验,当你把放置成朝向实验仪器东面和把实验仪器转了180°面向西面时,二者得出的物理规律也是一样的,所以空间旋转对称性对应的是角动量守恒。
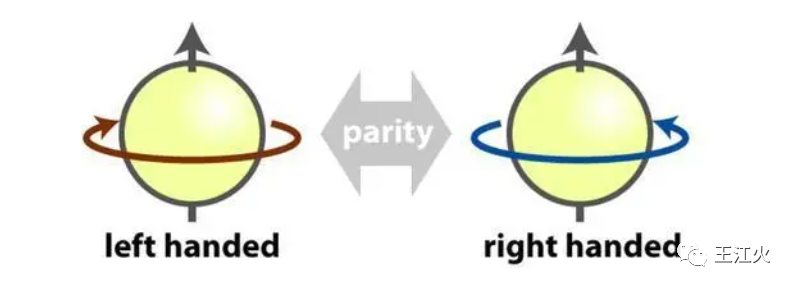
讲完了三个对称后,终于来到了今天的主角,也就是镜像对称。镜像对称也十分好理解。当你对着镜子举起你的左手时,镜子里的你会做一样的动作,而非抬起左腿。这种对称性对应的是宇称守恒,而科学家也一直坚信着这一观点,直到在1947年发现了θ粒子(sita),和τ粒子(tao)。
它们俩犹如亲身兄弟一样在质量,电荷等一切性质上都完全相同,那既然这样的话它们不应该是同一个粒子吗?但问题是,θ粒子和τ粒子,它们俩的衰变产物不一样。

这里举一个小例子说明什么是宇称。宇称是一个物理量,就和能量,动能一样。前面说到宇称和镜像对应,那么就可以用镜像的方式来理解。
首先顺时针转动一个小球,并把顺时针方向标为正,也就是+,并且规定数值为1,那么它的“旋转值”就是+1。而在镜子中,陀螺是逆时针旋转的,也就是负向的,所以它的“旋转值”就是-1。除了所谓的“旋转值”是相反之外,这两个小球完全相同。
虽然宇称并不是为了解释镜子里的世界,而是现实中的物理世界,只不过这样的例子比较好理解。

回到θ粒子和τ粒子的衰变产物,明显可以看出θ粒子和τ粒子的衰变产物分别是两个Π介子和三个Π介子,而Π介子的宇称数是-1。
通过简单的乘法运算,不难得出θ粒子的宇称数是+1,而τ粒子的宇称数是-1,也就是说τ粒子与θ粒子衰变时具有完全相反的宇称。
如果这么说很难理解的话,这个现象就好比说有两只小猪,无论从任何角度和方式去观察对比,它们都是完全一样的,但问题就出现在它们死后。两只小猪下肚后, 经过准确无比的计算,证实摄取的能量不一样,那么这两只小猪的生前肯定也不一样,毕竟能量是守恒的。这也被称为θ-τ之谜。
针对这个θ-τ之谜,总共有两种解释。一是相信θ粒子和τ粒子为两种不同的粒子,但科学家们始终无法确认为何θ、τ粒子性质如此相同,而第二种解释则是确认τ和θ是同一种粒,则宇称守恒定律不成立。
科学家们一直都在改进科研方式和器材,从而彻底剥开θ-τ的迷雾。但是这个问题直到1956年杨振宇和李政道等人提出了宇称不守恒后才彻底解决。
(未完待续)

本文完
本文共1900字,感谢读完,如果喜欢请三连,十分感谢您的支持。
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777