01 引言
为加深研究者对效应量及其置信区间的理解,同时便于研究者准确计算和报告效应量及其置信区间,本文首先介绍效应量的置信区间及其优势,然后以常用的效应量Eta squared(η²)为例,介绍其置信区间的原理及如何在开源软件(如R和JASP)中实现。
02 η²置信区间计算的原理
要理解η²的置信区间,需要理解与其相关参数有关的非中心性分布。在这里,η²置信区间的建构需要方差分析中F值的分布以及方差分析中另一个效应量指标Cohen’s f。以最简单的单因素被试间设计方差分析为例,其总体变异可以被分解成为组间变异和组内变异:
即:
其中X表示观测值,j表示分组水平(共有k组),n表示组内被试数量(每组内均有n个被试)。此时,F值计算公式如下:
(2.1)
其中
。此时组间处理的效应量为:
(2.2)
组间效应的另一种效应量指标——Cohens’f则可以通过如下公式计算:
(2.3)
此时的F分布和卡方分布存在非常紧密的关联。根据卡方分布的定义可知,卡方分布是从标准正态分布中独立抽取出样本的平方和的分布。也就是说,假设有p个从标准正态分布(N(0,1))中抽取出来的随机变量集合{
},则有:
这是一个自由度为k-1的卡方分布,且这个卡方分布是中心性的(注意,这里的中心性并非指的是该分布是中心对称,而是说其是从中心对称的分布中抽出来的数据的平方和的分布)。对照之前方差分析中F值的计算公式,如果将分子和分母同时除以
(处理引起的变异)和
(误差引起的变异)(在ANOVA的H0为真的情况下,假设处理变异同误差引起的变异相同即
,所以在公式中相互抵消了),则F值(F(df1,df2),以下简写为F)的分子和分母分别对应一个卡方分布。
在ANOVA中,由虚无假设为组间均数相等,实验误差服从正态分布N(0,
)可知,此时的分子分母对应的卡方分布是中心性。在此这情况下,F分布也呈中心性。
当虚无假设为假的时候,组间均数不相等,分子对应的卡方分布呈非中心性,分母作为实验误差对应的分布还是中心性的卡方分布。此时的F分布也变成了非中心性的,可以表示为F(df1,df2,δ)。实际上,中心分布是非中心分布的特殊情况。非中心参数ncp决定了分布的具体形态,例如中心F(2,52,ncp = 0)分布(黑色)和非中心F(2,52,ncp = 1)分布(红色),如下图所示。
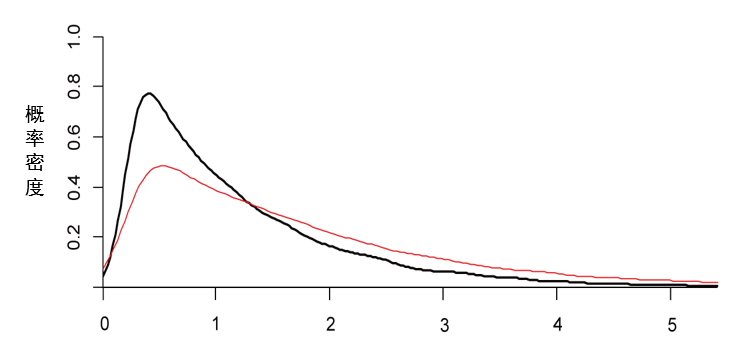
图1 中心F分布和非中心F分布
计算效应量的前提就是承认H0为假(组间均数不相等),其对应的F分布是非中心分布。如果计算η²的置信区间是基于非中心F分布,则其区间估计的上下限过程中,存在与Cohen’s d置信区间估计过程中同样的问题:在置信区间的上限与下限位置的F分布的非中心参数不相同。因此,对于η²的置信区间的估计,同样需要使用反演原(inversionconfidence interval principle)。
我们通过三个阶段得到置信区间:统计检验→中心参数→效应量统计。首先我们需要建立统计检验值(方差分析下的F值)和非中心参数以及效应量η²之间的关系。由公式2.2可得
,因此,可以推出
(2.4)
当虚无假设为假时,F(df1,df2)的非中心参数的估计值δ(非中心参数的符号表述方式可能会有不同,常用的符号包括δ、λ)的计算公式如下:
(2.5)
结合公式(2.4),我们得到非中心参数的估计:
(2.6)
至此我们建立起了统计值F和非中心参数之间的关系。再综合公式(2.1),(2.2)和(2.6),可以推断出η²与
和非中心参数δ的关系如下:
(2.7)
至此,我们得到了η²与F值、F分布的非中心参数之间的关系。接下来,我们就可以使用置信区间反演原理来计算η²的置信区间。假设给定我们一个样本F(5,194),我们需要构建一个100(1-α)%(α=0.05)的双侧的置信区间(如图2所示)。
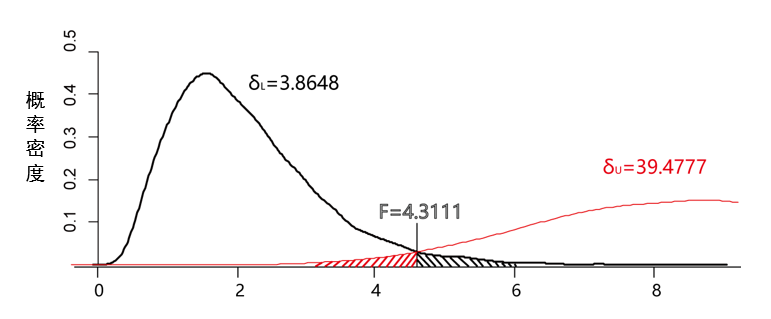
图2 构建η²置信区间的示例图
下限
对应F(5,194)右侧的α/2处,上限
对应F(5,194)左侧的α/2处。在得到与上下限对应的非中心参数δ后,我们可以将其转换为η²的置信区间,转换公式如下:
(2.8)
(2.9)
这样我们就完成了对η²的置信区间的估计。
值得注意的是,对ANOVA效应量置信区间的计算,通常报告90%的置信区间即可。原因在于均值之间的差异可以是正值也可以是负值,但是由于η²或R²是平方值,所以只有正值。计算95%的置信区间时,可能会得到包含0的置信区间,但此时p值可能小于.05,此时置信区间的结果与p值出现了矛盾(见 Karl Wuensch 的解释:
)。
而且Steiger(2004)指出均值比较的95%置信区间和90%置信区间得到的检验效力是一样的,并且η²不可能小于0,所以与0不存在显著差异的置信区间(通常情况下不包含0)的下限至少要从0开始。
03η²及其置信区间在R上的实现
将采用由JASP提供的样例数据来演示如何使用R计算η²的90%CI。该数据名为ToothGrowth和Bugs,分别用来展示被试间设计和被试内设计方差分析中η²及其CI的实现(SPSS上如何实现,见:)。
3.1被试间设计η²及其置信区间在R上的实现
Tooth Growth数据来自两因素完全随机设计,60只豚鼠被随机分配到6种处理条件下,用以研究不同类型的营养品(维生素C即VC和橙汁OJ)在不同抗坏血酸剂量条件下(0.5mg、1mg和2mg)对豚鼠牙齿生长的影响,因变量选取的是豚鼠牙齿的长度。
首先使用统计软件获得计算置信区间所需的统计值。这里你可以使用R中自带的函数aov或者一些带统计功能的工具包(如ez、car等等),这里需要注意的是用R进行方差分析时,不同的工具包或者函数使用的平方和类型会有所不同,例如aov函数进行计算的时候默认使用的是Type I SS(sun of square),ezANOVA默认使用的是Type II SS(可以在R中使用type对平方和类型进行调整,详见),而SPSS在进行方差分析计算的时候默认的是Type III SS(可以在SPSS中模型选项进行调整)。当数据不同组间的被试量相同时,不同类型平方和计算结果出现的差异不大,但是当数据不平衡的时候,则要谨慎考虑平方和类型,因为不同的平方和类型会带来不同的统计结果,感兴趣的读者可以参考(Langsrud,2003)。当然更为便捷的办法是应用JASP直接进行统计分析并获得相应的统计值。例如对于以上数据,可得F(2,54)= 92,随后在R中下载并打开MBESS工具包,输入相关的统计值进行置信区间的计算,R中的命令如下:
library(“MBESS”)ci.pvaf(F.value=92,df.1=2,df.2=54,N=60,conf.level=.90)
3.2被试内设计η²及其置信区间在R上的实现
Bugs数据来自两因素混合设计,用以研究不同性别(男、女)人群对于不同类型(不吓人不恶心、不吓人很恶心、很吓人不恶心和很吓人很恶心)虫子图片的敌意指数,并采用10点评分表明想要杀死或者驱赶虫子的程度(Ryan,Wilde, & Crist, 2013)。通过JASP,我们可以得到F(2.64,224.48),(注意被试内设计数据在违背球形假设的情况下使用校正后的自由度)。然后再R中使用如下命令得到置信区间:
#打开MBESS工具包library(“MBESS”)#输入F值及自由度Lims<-conf.limits.ncf(F.value=20.14,conf.level=0.90,df.1=2.64,df.2=224.48)#计算90%置信区间的下限Lower.lim<-Lims$Lower.Limit/(Lims$Lower.Limit+df.1+df.2+1)#计算90%置信区间的上限Upper.lim<-Lims$Upper.Limit/(Lims$Upper.Limit+df.1+df.2+1)
3.3 结果报告与解释
对于η²及其置信区间的解释主要参照η²的定义,也就是实验效应引起的变异占总体变异的比例,因此η²的大小说明了在具体的实验研究中对于自变量操作的有效性。也就是说η²越大,相关变量之间的关系越紧密,当然这种关系的属性,即相关还是因果关系主要由实验设计的类型(如准实验设计和实验设计)决定。但是由于η²置信区间不可能小于0,这也就决定了对于η²的解释不可能像Cohen’sd 的置信区间一样,把包含0的置信区间作为我们拒绝或者接受零假设的依据。而且方差分析的应用作为一般线性模型下的特例,往往只是对涉及变量间关系检验的第一步。因此我们一般把η²及其置信区间作为评价实验变量操控有效性的指标,接下来具体的组间比较才是研究者关注的重点(例如主效应显著后的多重比较、交互作用显著后的简单效应分析),而在组间比较中可以再次使用如t检验下的Cohen’sd作为评价组间差异可靠性的效应量指标。
参考文献:
王 珺, 宋琼雅, 许岳培, 贾彬彬, 胡传鹏, . 效应量置信区间的原理及其实现[J]. 心理技术与应用, 2019, 7(5): 284-296.
作 者:王珺、宋琼雅 、许岳培、贾彬彬、胡传鹏
编 辑:钟妤
校 对:胡传鹏、方圆、张馨新、念靖晴
注:本文编辑是通过“”进入公众号运营团队,如果你想致力于开放科学的推广,可点击上方绿色字体查阅报名方式。
OpenScienceClub
Makepsychologyopenandtrustworthy!
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777






