Log-rank检验和比例风险Cox模型是常用于分析时间-事件(Time-to-event, TTE)变量的方法。
火影这部漫画作品讲述了小鸣和小佐两位背负着不同命运的主人公,从小不点儿成长为能够独当一面的出色忍者的、充满了爱恨情仇的故事。
图1 小鸣和小佐
自小便无人管束的小鸣从刚入学时的“吊车尾”一路成长为了忍界中拥有最强战力的木叶村的村长,而在精英教育下成长的天才小佐最后也超越了忍界精英贵族史上最强统领者,暗中守护木叶村。小鸣和小佐究竟谁更胜一筹,一直是火迷们茶余饭后津津乐道的话题之一。假设小鸣和小佐一生中面对的敌人总数几乎相同,分别为N1和N2,二人在t1,t2,…,tK的时间点被f1,f2,…,fK个敌人击败,其中在第k个时间点tk,小鸣和小佐分别被f1k和f2k个敌人击败。这是一个时间-事件数据(至被敌人打败的时间),我们是否可以考虑通过时间-数据的分析方法(即log-rank检测和Cox模型)比较小鸣和小佐的实力呢?回想前期小文“”,我们可以分别画出小鸣和小佐对阵敌人的KM曲线,以小鸣为例,若小鸣被敌人击败一次,则小鸣的KM曲线向下降一格,若获胜则KM曲线维持原高度;利用log-rank检验即可获知两条KM曲线的差异,用Cox模型即可算出小鸣较小佐被敌人击败的风险比(HR);如果log-rank检验所得p值越小,且HR值和1的差值的绝对值越大,则小鸣和小佐间实力差距越大。
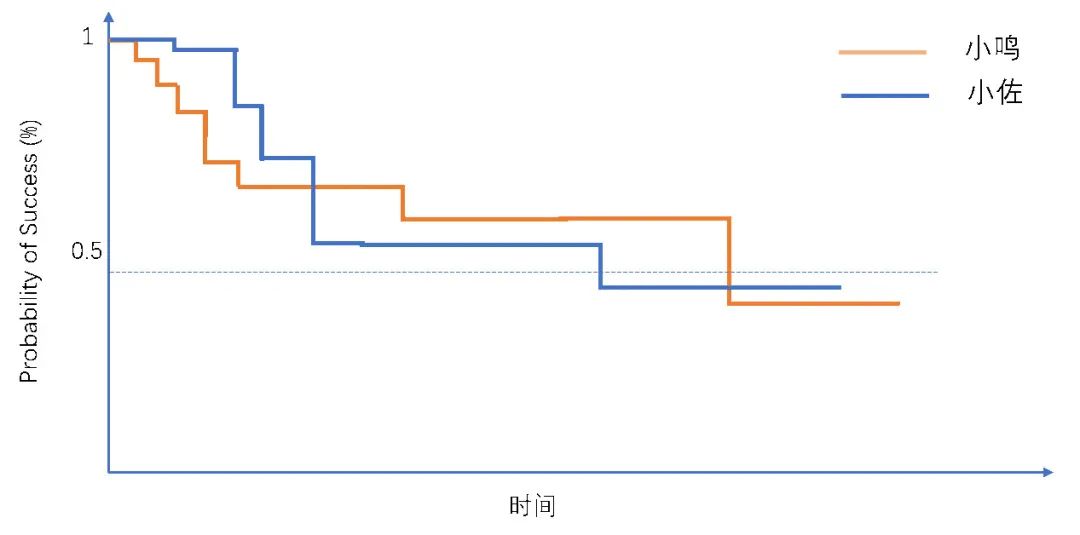
图2 小鸣、小佐对阵敌人胜败情况的KM曲线
log-rank检验工作原理
这里需要强调的是,log-rank法是非参数检验法(仅依赖于观察到的数据,而不需引入其他参数),该法通过计算tk(k=1,…,K)时,小鸣被敌人击败的可能性与二人总体上被击败的可能性的差值diffk(p小鸣被击败 -E( p二人被击败)),diffk > 0,则说明在k时刻小鸣的实力在小佐之下,反之则该时刻小鸣的实力在小佐之上。在二人成长过程中,各时间点的差值总和为Diff = diff1 + diff2 + … +diffK-1 + diffK,若Diff为正值,则说明整体上小鸣较小佐表现逊色,反之,则说明小鸣的表现更为优秀。Diff的绝对值越大,则小佐和小鸣实力的差距越大。这也是log-rank检验工作的原理。
在双臂平行对照研究中,只需计算出试验组在各关键时间点(试验组和对照组发生事件的所有时间点)发生事件的风险概率相较于两组期望的风险概率的差值(diffj),并加和得到Diff。若Diff> 0,则表明试验组较对照组疗效差,反之则试验组较对照组疗效好。此差值的绝对值越大,两组疗效的差异越大(方差相同的情况下)。所以log-rank检验是通过对发生事件的每个时间点的两组风险概率与预期风险概率差值进行加和比较,差值越大,两组差异越大。
cox模型工作原理
下面我们通过小鸣和小佐的例子看看Cox模型是如何工作的。假设小鸣较小佐实力的比值是一个不随时间变化的常数φ,即小鸣较小佐在各个时间点被敌人击败的风险(h小鸣/h小佐)为不随时间变化的常数β = 1/φ(实力越强则被敌人打败的风险越低,故而被敌人打败的风险比值是实力比值的倒数)。我们通过各个时间点击败小鸣和小佐的敌人数量猜测β可能的取值β^。如果该值>1则说明小鸣在各个时间点战败的可能性高于二人战败的平均水平,因此小佐较小鸣优秀,反之则小鸣不比小佐差。这和Cox模型的工作原理异曲同工。Cox模型是一种半参数模型(除了利用观察到的数据外,还需要引入参数β进行模型拟合),通过小鸣和小佐的例子可以看出,其应用有一定的前提假设,即要求在各个时间点风险因素不同的受试者发生事件的可能性是等比例的。很显然,如果小佐和小鸣实力在各个时间点的比值并不是常数,甚至有时>1(小佐优于小鸣),有时候
通常一张随机对照研究(RCT)的常规KM图上除了各治疗组的KM曲线外,还会利用文字标示各组的中位生存时间和95%置信区间以及试验组较对照组的风险比及其95%CI,有时也会标上log-rank检验的p值。(如图3)
图3 KM曲线示例(摘自ESMO 2022,Camrelizumab plus rivoceranib vs.sorafenib as first-line therapy for unresectable hepatocellular carcinoma:a randomized, phase 3 trial, Shukui Qin et.al.)
Cox模型和log-rank检验有何关系呢?
在符合比例风险的假设时,log-rank检验和Cox model在检出对照组间风险差异时都非常高效;一般来说,当Hazard ratio估计值小于1且其95% CI的上限也小于1时/或Hazard ratio >1且其95% CI的下限大于1时,log-rank检验的p值也小于0.05。在明显违背比例风险假设时,Cox model和log-rank test有可能提示不同的结果。
如何判断比例风险假设是否成立呢?
我们可以通过以下方法对比例风险假设成立与否进行判别:
1)分别绘制各组的累计风险随时间变化的曲线(对数转换),如果各组的曲线平行,则比例风险假设成立(图4A);
2)看Schoenfeld残差是否随机分布在y=0参考线的周围(图4B);
图4 判断比例风险假设是否成立(图片来自网络)
(点击可放大)
3)在Cox模型中加入时间依赖项,看该项是否对模型有显著的贡献。
更直观的方法是观察两条KM曲线的关系。违背等比例风险假设的KM曲线例子包括但不限于,随着时间的推移,KM曲线相交/靠近一次或多次、KM曲线先分开再合并、KM曲线先合并再分开等。如图5B、5C和5D。
图5 Non-proportional hazard下的KM曲线(Andrea Knezevic & Sujata Patil, Memorial Sloan Kettering Cancer Center, SAS global forum 2020)
在违背等比例风险的情况下,log-rank检验和Cox model得出的结果是不可靠的,有可能低估实际的风险比。
应该如何分析该类不符合等比例风险假设的数据呢?
首先,我们可以考虑分时间段处理:由于考虑到小鸣在进入忍者学校前无人管束,因此酌情降低佐鸣忍者学校期间的权重,而酌情升高二人成为正式忍者之后,尤其是师从蛇叔和自来也后的权重,即差值总和Diff=w1diff1+w2diff2+…+wj-1diffj-1 + wJdiffJ,其中wj为每个关键时间点的权重。引申到生存数据即为对不同时间点进行权重调整的weighted log-rank test。在weighted log-rank检验的基础上,可构建复合检验对治疗组间发生事件的风险差异比进行检验。
此外,我们也可以比较某一时刻前,小鸣和小佐KM曲线下的面积,若小鸣KM曲线下面积大于小佐,则说明整体而言小鸣的实力略胜一筹。这便是restricted mean time survival(RMST)模型,通过比较特定时间点前两条KM曲线下/或拟合的生存曲线面积的差异来检验不同的干预之间是否具有发生事件风险的差异并籍此估算风险比。
下面,我们来看两个化腐朽为神奇的例子,NOTABLE研究和NALA研究。
NOTABLE研究(尼妥珠单抗+吉西他滨 vs. 吉西他滨单药在局部晚期或转移性胰腺癌中的前瞻性、随机对照、双盲、多中心的Ⅲ期研究)以OS为主要研究终点。该研究的OS曲线如图6,可见在随机后的约8个月内,两条KM曲线基本重合,而后慢慢分开,是典型的违背等比例风险假设的曲线,尤其是在50%生存概率的参考线处,两条曲线刚刚开始小幅度分开。因此研究采用了RMST法估算HR并检验组间差异,结果提示两药联用的效果优于单药。
图6Nimo+Gem vs. Placebo + Gem (摘自ShuKui Qin. et al. ASCO 2022 LBA 4011)
此处,我们也回顾一下NALA研究。NALA研究是一项奈拉替尼在晚期HER2阳性乳腺癌三线及以上研究,该研究允许纳入脑转移的受试者。其主要研究终点为PFS和OS。下面以PFS的终点为例,在6个月前,两条KM曲线几乎完美重合,常规方法估算的中位KM时间基本相同。而是用RMST之后,我们更关注整个研究过程中KM曲线下面积的差异(即标橘粉色部分),我们可以看到其中位PFS时间出现了差异,分别为8.8个月和6.6个月,p值也较log-rank检验的p值更小。由于该研究通过预先设定α分配的方式控制整体I类错误,虽然该研究的OS没有成功,但该研究依然支持了奈拉替尼在晚期HER2+乳腺癌多线治疗的获批。
图7 NALA研究的PFS(Cristina Saura. et al., JCO 38, 2020)
除了以上两种方法外,还可以使用加速时间模型等方法处理风险非等比例的数据。那么这些针对非等比例风险数据的检验方法各有什么优缺点呢?且听下回分解。
总结一下,log-rank检验和Cox模型是分析不同组别时间-事件终点的差异的经典方法。但只有在符合等比例风险假设的情况下,其检验效能和准确性才最高。故而我们在对时间-事件类型的终点进行分析前,应当事先对比例风险假设进行验证,若数据明显违背等比例风险假设,可采用weighted log-rank test, RMST等方法对数据进行分析。
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777






