如今,期刊论文中的模型较以往更加复杂。比如结合了中介与调节的模型、多重中介模型、多层模型等。单一中介或调节模型由于结构较为简单,往往很少使用。
今天我们介绍一个复杂度中等偏低的模型,即2-way交互模型。该模型在原有单一调节模型的基础上,又增加了一个调节变量。
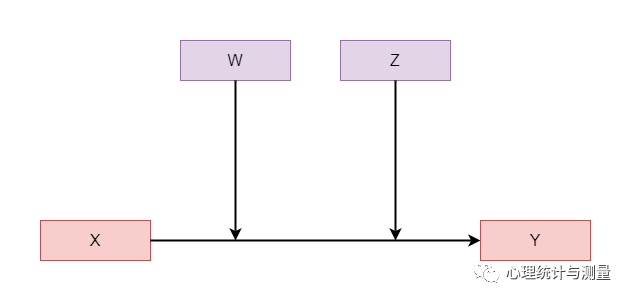
在上图中,W与Z同时调节了X与Y之间的关系,但X与Z之间并没有交互关系。这时候,X与Y之间的关系随着W与Z的变化而变化。
所有的变量均为显变量。
与往常一样,根据模型图来绘制统计图以便于写方程。

在2-way交互模型中,所有的路径都指向因变量Y。
除了W的主效应外,X与W的交互项XW也对Y有影响。另一个调节变量Z也是一样,除了主效应外,还有一个与X的交互效应b5。
Y的方程:
Y = b0 + b1X + b2W + + b3Z + b4XW + b5XZ将方程写成Y=aX+b的形式:
Y = (b0 + b2W + b3Z) + (b1 + b4W + b5Z)X斜率项为:
b1 + b4W + b5Z此斜率项能够看出X与Y的关系的确如前所述,是随着W与Z的变化而变化的。它也为后面画斜率图做准备。
开始写Mplus代码
先从标题(Title)开始,给代码脚本取个名字,方便以后使用时不会混淆,也方便查找。
其次,写出数据(Data)文件保存的具体路径。
注意:如果在写完代码后将.inp为后缀的代码文件保存在存放原始数据的文件夹中,就无需写出数据文件的具体路径(如C:/My data/data),直接写出原始数据文件的文件名即可(如data.csv)。
TITLE: two moderators, 2-way interactions with x only;DATA: FILE IS data.csv;
在VARIABLE中说明数据文件中所包含的指标名称,指标名称的顺序要与原始文件一致。
USEVARIABLES指本次分析需要使用到哪些指标。像被试ID这列变量我们用不到,就不必写在USEVARIABLES里。
VARIABLE: NAMES ARE ID X W Y;USEVARIABLES = X W Y XW XZ;
虽然原始数据文件并没有XW与XZ的交互项,但在USEVARIABLES命令中必须呈现出来。
定义交互项
DEFINE:XW = X*W;XZ = X*Z;
分析时可以使用bootstrap以降低抽样误差带来的影响
ANALYSIS:TYPE = GENERAL;ESTIMATOR = ML;= 5000;
用ON阐明变量之间的关系,用法:
因变量 ON 自变量 (系数)
MODEL:[] (b0); ! 截距项b0Y ON X (b1);Y ON W (b2);Y ON Z (b3);Y ON XW (b4);Y ON XZ (b5);
使用MODEL CONSTRAINT命令
用NEW生成新系数。
模型有2个调节变量W与Z,因此要生成它们在高低水平下的值共2*2=4个(低W,高W,低Z,高Z)。此外,W与Z共有4种不同组合,分别是:
低水平W-低水平Z
高水平W-低水平Z
低水平W-高水平Z
高水平W-高水平Z
MODEL CONSTRAINT:NEW(LOW_W HIGH_WLOW_Z HIGH_ZLOW_LOZ HIW_LOZ LOW_HIZ HIW_HIZ);LOW_W = W在低于一个SD时的值;HIGH_W = W在低于一个SD时的值;LOW_Z = Z在低于一个SD时的值;HIGH_Z = Z在高于一个SD时的值;
W与Z在高低水平上的4个值需要自行提前计算好填入上面的语句中。可用SPSS计算。
接下来要计算在W与Z的不同水平下,Y的斜率是怎样的?
还记得之前关于Y方程的斜率项吗?
b1 + b4W + b5Z ! 斜率项这里终于将它派上用场了!我们需要计算4种情况下的斜率,分别是:
低水平W-低水平Z组合时,Y的斜率(LOW_LOZ)
高水平W-低水平Z组合时,Y的斜率(HIW_LOZ)
低水平W-高水平Z组合时,Y的斜率(LOW_HIZ)
高水平W-高水平Z组合时,Y的斜率(HIW_HIZ)
LOW_LOZ = b1 + b4*LOW_W + b5*LOW_Z;HIW_LOZ = b1 + b4*HIGH_W + b5*LOW_Z;LOW_HIZ = b1 + b4*LOW_W + b5*HIGH_Z;HIW_HIZ = b1 + b4*HIGH_W + b5*HIGH_Z;
斜率计算好了,可以绘图啦!
绘图既需要斜率,还需要截距。还记得截距是什么吗?回顾下Y的方程:
Y = (b0 + b2W + b3Z) + (b1 + b4W + b5Z)X同样,按照W与Z的四种组合写出Y的4个方程:
低水平W-低水平Z组合时,Y的方程(FLOW_LOZ)
高水平W-低水平Z组合时,Y的方程(FHIW_LOZ)
低水平W-高水平Z组合时,Y的方程(FLOW_HIZ)
高水平W-高水平Z组合时,Y的方程(FHIW_HIZ)
PLOT(FLOW_LOZ FHIW_LOZFLOW_HIZ FHIW_HIZ);LOOP(X,1,7,0.1);= (b0 + b2*LOW_W + b3*LOW_Z) + LOW_LOZ*X;= (b0 + b2*HIGH_W + b3*LOW_Z) + HIW_LOZ*X;= (b0 + b2*LOW_W + b3*HIGH_Z) + LOW_HIZ*X;= (b0 + b2*HIGH_W + b3*HIGH_Z) + HIW_HIZ*X;PLOT:TYPE = plot2;
告诉PLOT绘制4条线
在LOOP中说明,以X为横轴,0.1为步长,从1到7绘制图形。
起点与终点可根据问卷题项的全距进行相应地调整。例如,如果X是Likert五点量表计分,那么LOOP里的参数可写成:
LOOP(X,1,5,0.1)最后,输出结果。这里我们需要标准化结果以及bootstrap后系数的置信区间。
OUTPUT:STDYX CINT(bcbootstrap);
附2-way interactions的语句简版:
TITLE: two moderators, 2-way interactions with x only;DATA: FILE IS data.csv;VARIABLE: NAMES ARE ID X W Y;USEVARIABLES = X W Y XW XZ;DEFINE:XW = X*W;XZ = X*Z;ANALYSIS:TYPE = GENERAL;ESTIMATOR = ML;BOOTSTRAP = 5000;MODEL:[Y] (b0); ! 截距项b0Y ON X (b1);Y ON W (b2);Y ON Z (b3);Y ON XW (b4);Y ON XZ (b5);MODEL CONSTRAINT:NEW(LOW_W HIGH_WLOW_Z HIGH_ZLOW_LOZ HIW_LOZ LOW_HIZ HIW_HIZ);LOW_W = W在低于一个SD时的值;HIGH_W = W在低于一个SD时的值;LOW_Z = Z在低于一个SD时的值;HIGH_Z = Z在高于一个SD时的值;LOW_LOZ = b1 + b4*LOW_W + b5*LOW_Z;HIW_LOZ = b1 + b4*HIGH_W + b5*LOW_Z;LOW_HIZ = b1 + b4*LOW_W + b5*HIGH_Z;HIW_HIZ = b1 + b4*HIGH_W + b5*HIGH_Z;PLOT(FLOW_LOZ FHIW_LOZFLOW_HIZ FHIW_HIZ);LOOP(X,1,7,0.1);FLOW_LOZ = (b0 + b2*LOW_W + b3*LOW_Z) + LOW_LOZ*X;FHIW_LOZ = (b0 + b2*HIGH_W + b3*LOW_Z) + HIW_LOZ*X;FLOW_HIZ = (b0 + b2*LOW_W + b3*HIGH_Z) + LOW_HIZ*X;FHIW_HIZ = (b0 + b2*HIGH_W + b3*HIGH_Z) + HIW_HIZ*X;PLOT:TYPE = plot2;OUTPUT:STDYX CINT(bcbootstrap);
参考文献:
Stride, C.B., Gardner, S., Catley, N. & Thomas, F.(2015) 'Mplus code for the mediation, moderation, and moderated mediation model templates from Andrew Hayes' PROCESS analysis examples', http://www.offbeat.group.shef.ac.uk/FIO/mplusmedmod.htm限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777






