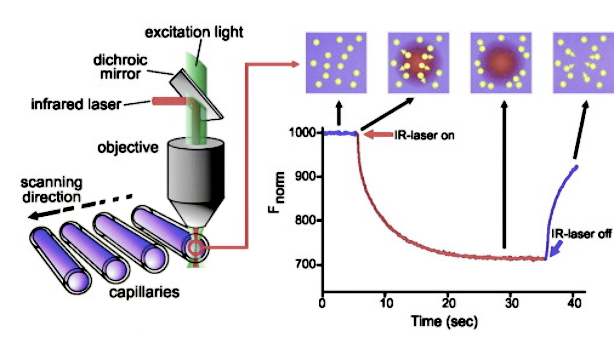
论文标题: Continual Learning on Noisy Data Streams via Self-Purified Replay
论文链接:
代码:
引用:Kim C D, Jeong J, Moon S, et al. Continual learning on noisy data streams via self-purified replay[C]//Proceedings of the IEEE/CVF international conference on computer vision. 2021: 537-547.
导读
在真实世界中进行持续学习必须克服许多挑战,其中标签带噪是一个常见且不可避免的问题。在这项工作中,我们提出了一个基于重放的持续学习框架,同时解决灾难性遗忘和噪声标签的问题。
我们的解决方案基于两个观察结果:(i) 即使通过自监督学习,使用噪声标签也可以减轻遗忘,并且(ii)重放缓冲区的纯度是至关重要的。基于此,我们提出了我们方法的两个关键组成部分: (i) 一种名为自重放的自监督重放技术,它可以规避由噪声标记数据产生的错误训练信号;(ii)一个自中心的滤波器,通过基于中心的随机图集合来维护干净的重放缓冲器。
在MNIST、CIFAR-10、CIFAR-100和WebVision上的实证结果表明,我们的框架可以在噪声流数据中保持高纯度的重放缓冲区,同时大大优于最先进的持续学习和噪声标签学习方法的组合。
本文贡献本文方法
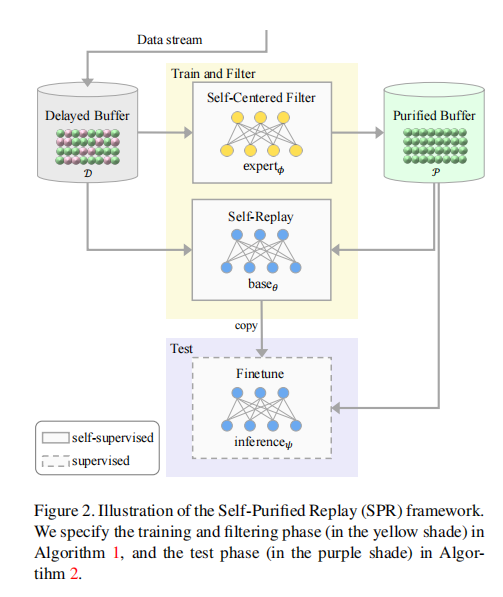
图2描绘了由两个缓冲区和两个网络组成的框架。 Delayed buffer D 临时存储传入的数据流,而 Purified buffer P 维护经过净化的数据。基础网络通过自监督重放(Self-Replay)训练处理灾难性遗忘。专家网络是 Self-Centered 过滤器的关键组件,通过中心性获取有信心的干净样本。两个网络具有相同的体系结构(例如,ResNet-18),但具有不同的参数。算法1概述了训练和过滤过程。每当延迟缓冲区 D 满时,由专家网络驱动的 Self-Centered 过滤器从D中筛选出干净样本并将其存储到干净缓冲区P中。然后,基础网络通过对 D ∪ P 中的样本进行自监督损失进行训练。在学习的任何阶段,我们可以通过将基础网络复制到推理网络、添加最终的softmax层并使用P中的样本进行微调,来执行下游任务(即分类)。算法2概述了这个推理阶段。

Self-Replay
当训练集中存在错误配对x和y时,使用有噪声标记数据会导致错误的反向传播信号。因此,我们通过仅从 x(没有 y)进行学习,使用对比自监督学习技术来避免这种错误。也就是说,该框架首先通过对所有传入的 x 进行自监督学习来专注于学习通用表示。随后,下游任务(即监督分类)使用仅在干净缓冲区 P 中的样本微调表示。在持续学习的术语中,基于这一概念形成了 Self-Replay,通过对延迟和干净缓冲区中的样本(D ∪ P)进行自监督重播,减轻了遗忘同时学习通用表示。
具体地说,我们在基础网络的平均池化层上添加了一个投影头 g(·)(即一个单层MLP),并使用归一化的温度尺度交叉熵损失[12]对其进行训练。对于来自 D 和 P 的批大小分别为 Bd,Bp∈N的小批,我们应用随机图像转换(例如,裁剪,颜色抖动,水平翻转)来创建每个样本的两个相关视图,称为正样本。然后,优化损失以使正样本的特征彼此更加接近,同时使它们与批次中的其他样本相互排斥,称为负样本。更新的目标变为:
(xi, xj) 表示为正样本,将 xk 表示为负样本。
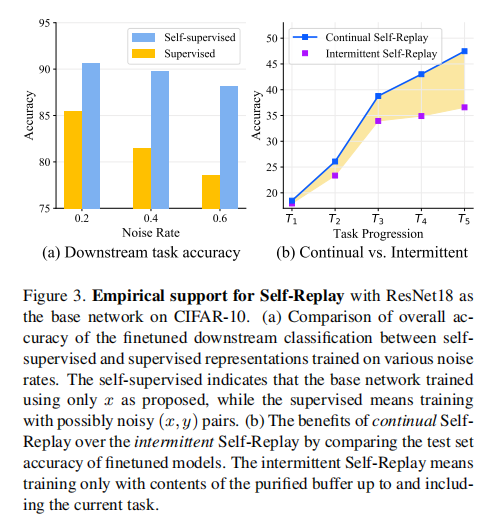
图 3 展示了关于 Self-Replay 在带有噪声标签的持续学习中有效性的一些经验结果。
图 3(a) 对下游分类任务进行了定量检查。它表明自监督学习导致更好的表示,最终在性能上优于显著较大的有监督学习。
图 3(b) 举例说明了 Self-Replay 在持续学习中的优越性。我们将 Self-Replay(如所提出的)的持续训练与间歇性训练的 Self-Replay 进行对比,后者仅在每个任务结束时离线训练,只使用干净缓冲区中的样本。图 3(b) 中的彩色区域显示了持续学习的表示如何减轻遗忘并有助于过去和未来任务之间的知识转移。
Self-Centered Filter
Self-Centered filter 的目标是获得可靠的干净样本;具体来说,它将干净的概率分配给延迟缓冲区中所有样本的概率。
专家网络。专家网络用于为延迟缓冲区中的样本提取特征。这些特征用于计算样本的中心性,这是选择干净样本的标尺。受 Self-Replay 中自监督学习良好表示成功的启发,专家网络也使用 Eq. 1 中的自监督损失进行训练,唯一的区别是我们仅使用 D 中的样本(而不是 D ∪ P 中的样本)。
中心性。Self-Centered filter 的核心是中心性 [59],它植根于图论,用于识别图中最有影响力的顶点。我们使用特征网络的余弦相似性来构建每个类别的延迟缓冲区中唯一类别标签的加权无向图 G := (V, E)。我们假设干净样本形成每个类别图中最大的簇。每个顶点 v ∈ V 是类别的一个样本,边 e ∈ E 的权重是专家网络特征之间的余弦相似度。对于邻接矩阵
。然后,将该图的主要特征值归一化为单位长度,得到归一化的中心性向量 :
最终的中心性向量 c 是专家网络输出样本的权重。
Beta混合模型。中心性量化了在相同类标签的数据中哪些样本最有影响力(或最干净)。然而,相同标签的数据包含干净和带有噪声标签的样本,其中带有噪声的样本可能欺骗性地操纵中心性分数,导致对干净和噪声样本的中心性分数的不明确划分。因此,我们通过将Beta混合模型(BMM)[33]拟合到中心性分数来计算每个样本的清洁概率,即:
由于中心性分数的偏斜性质,Beta分布是p(c|z)的一个合适选择。我们设置 Z = 2,表示干净和噪声组件,这在准确性和计算成本方面经验性上是最佳的。我们使用EM算法[15]拟合BMM,通过它我们得到后验概率:
在Z = 2组件中,我们可以很容易地将干净的组件识别为c分数较高的组件(即,一个更大的簇)。然后,干净的后验 p(z = clean|c) 定义了中心性 c 属于干净组件的概率,该概率用作进入和退出干净缓冲区 P 的概率。在选择的样本进入我们的完整干净缓冲区后,根据最低的 p(z = clean|c) 采样出样本。
随机集成
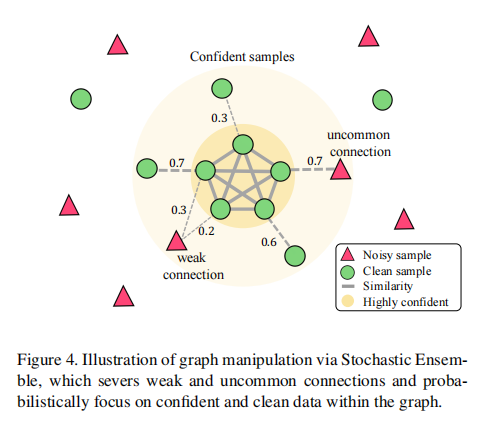
由于我们的目标是尽可能地获取最干净的样本,我们希望进一步筛选可能带有噪声的样本。我们通过引入BMM的随机集成来实现这一点,使 posterior 比前一节中的非随机 posterior p(z = clean|c) 更具噪声鲁棒性。
首先,我们通过从 A 上的伯努利分布中抽取多个二进制邻接矩阵 {A} 来为随机集成做准备。对于每个类别 l,我们在 A 上施加条件伯努利分布,如下所示:
我们发现将不同值截断为 0(ReLU)并使用余弦相似度值作为概率的方法在经验上是有帮助的。我们用一个小的正值替换 A 中的零以满足Perron-Frobenius定理的要求。然后,我们的重构的鲁棒后验概率是:
而 p(z|cent(A)) 可以以与前一节中的非随机 posterior 相同的方式获得。我们使用 Monte Carlo 抽样来近似积分,其中 E_max 作为样本大小。基本上,我们在不同的随机图上拟合混合模型,通过保留强大和密集的连接而切断弱或不常见的连接,以概率地剔除更有信心的噪声样本。这在图 4 中概念上进行了说明。
实验实验结果
与其他方法的比较:
结论
Self-Purified Replay(SPR)框架通过结合自监督学习的自回放技术来减轻遗忘和处理噪声标签信号,解决了噪声标记持续学习的挑战。Self-Centered filter 利用基于中心性的随机图集合,帮助维护一个干净的重放缓冲区。在合成数据集和真实噪声数据集上的实验结果表明,SPR可以在高噪声数据流存在的情况下有效地保持干净的重放缓冲区,超过了噪声标签学习和持续学习基线的各种组合。研究结果表明了利用自监督来同时解决持续学习和噪声标签问题的潜力。未来的工作可以探索扩展SPR,以保持不仅干净,而且更多样化的缓冲区。
☆ END ☆
如果看到这里,说明你喜欢这篇文章,请转发、点赞。微信搜索「uncle_pn」,欢迎添加小编微信「 woshicver」,每日朋友圈更新一篇高质量博文。
↓扫描二维码添加小编↓
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777