机器之心整理
参与:蒋思源
这是一套香港科技大学发布的极简TensorFlow入门教程,三天全套幻灯片教程已被分享到GoogleDrive。机器之心将简要介绍该教程并借此梳理TensorFlow的入门概念与实现。
该教程第一天先介绍了深度学习和机器学习的潜力与基本概念,而后便开始探讨深度学习框架TensorFlow。首先我们将学到如何安装TensorFlow,其实我们感觉TensorFlow环境配置还是相当便捷的,基本上按照官网的教程就能完成安装。随后就从「HelloTensorFlow」开始依次讲解计算图、占位符、张量等基本概念。
当然我们真正地理解TensorFlow还需要从实战出发一点点学习那些最基本的概念,因此第一天重点讲解了线性回归、Logistic回归、Softmax分类和神经网络。每一个模型都从最基本的概念出发先推导运行过程,然后再结合TensorFlow讲解张量、计算图等真正的意义。神经网络这一部分讲解得十分详细,我们将从最基本的感知机原理开始进而使用多层感知机解决异或问题(XOR),重点是该课程详细推导了前向传播与反向传播的数学过程并配以TensorFlow实现。
教程第二天详细地讨论了卷积神经网络,它从TensorFlow的训练与构建技巧开始,解释了应用于神经网络的各种权重初始化方法、激活函数、损失函数、正则化和各种优化方法等。在教程随后论述CNN原理的部分,我们可以看到大多是根据斯坦福CS231n课程来解释的。第二天最后一部分就是使用TensorFlow实现前面的理论,该教程使用单独的代码块解释了CNN各个部分的概念,比如说2维卷积层和最大池化层等。
教程第三天详解了循环神经网络,其从时序数据开始先讲解了RNN的基本概念与原理,包括编码器-解码器模式、注意力机制和门控循环单元等非常先进与高效的机制。该教程后一部分使用了大量的实现代码来解释前面我们所了解的循环神经网络基本概念,包括TensorFlow中单个循环单元的构建、批量输入与循环层的构建、RNN序列损失函数的构建、训练计算图等。
下面机器之心将根据该教程资料简要介绍TensorFlow基本概念和TensorFlow机器学习入门实现。更详细的内容请查看香港科技大学三日TensorFlow速成课程资料
TensorFlow基础
本小节将从张量与图、常数与变量还有占位符等基本概念出发简要介绍TensorFlow。需要进一步了解TensorFlow的读者可以阅读谷歌TensorFlow的文档,当然也可以阅读其他中文教程或书籍,例如《TensorFlow:实战Google深度学习框架》和《TensorFlow实战》等。
1.图
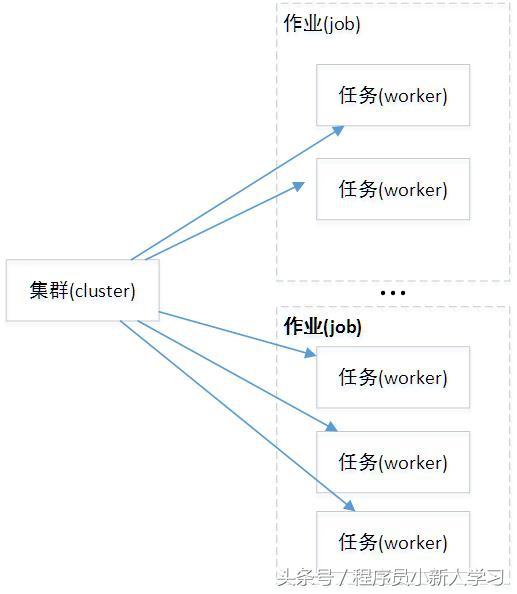
TensorFlow是一种采用数据流图(dataflowgraphs),用于数值计算的开源软件库。其中Tensor代表传递的数据为张量(多维数组),Flow代表使用计算图进行运算。数据流图用「结点」(nodes)和「边」(edges)组成的有向图来描述数学运算。「结点」一般用来表示施加的数学操作,但也可以表示数据输入的起点和输出的终点,或者是读取/写入持久变量(persistentvariable)的终点。边表示结点之间的输入/输出关系。这些数据边可以传送维度可动态调整的多维数据数组,即张量(tensor)。
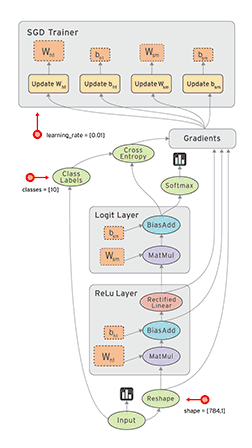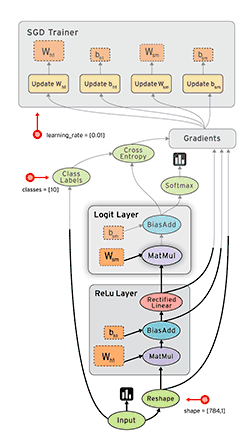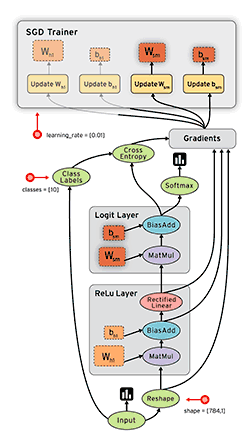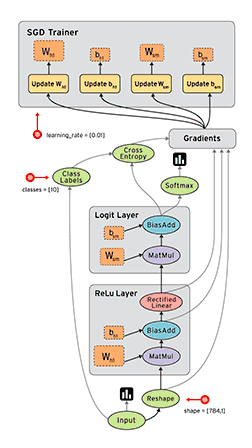
在Tensorflow中,所有不同的变量和运算都是储存在计算图。所以在我们构建完模型所需要的图之后,还需要打开一个会话(Session)来运行整个计算图。在会话中,我们可以将所有计算分配到可用的CPU和GPU资源中。
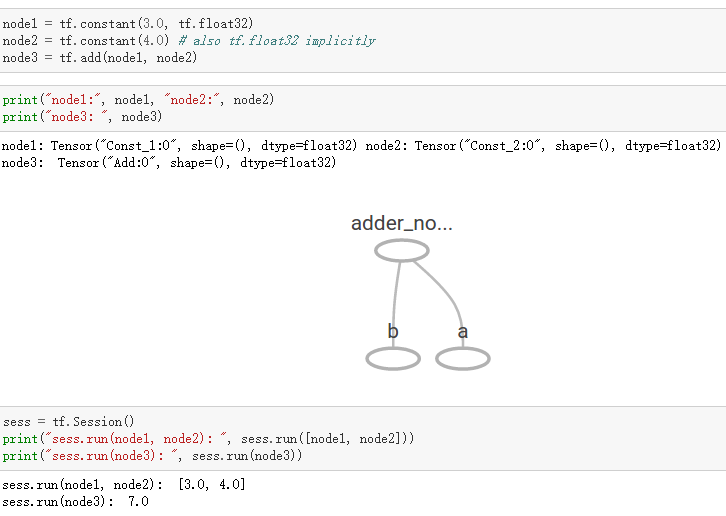
如上所示我们构建了一个加法运算的计算图,第二个代码块并不会输出计算结果,因为我们只是定义了一张图,而没有运行它。第三个代码块才会输出计算结果,因为我们需要创建一个会话(Session)才能管理TensorFlow运行时的所有资源。但计算完毕后需要关闭会话来帮助系统回收资源,不然就会出现资源泄漏的问题。
TensorFlow中最基本的单位是常量(Constant)、变量(Variable)和占位符(Placeholder)。常量定义后值和维度不可变,变量定义后值可变而维度不可变。在神经网络中,变量一般可作为储存权重和其他信息的矩阵,而常量可作为储存超参数或其他结构信息的变量。在上面的计算图中,结点1和结点2都是定义的常量tf.constant()。我们可以分别声明不同的常量(tf.constant())和变量(tf.Variable()),其中tf.float和tf.int分别声明了不同的浮点型和整数型数据。
2.占位符和feed_dict
TensorFlow同样还支持占位符,占位符并没有初始值,它只会分配必要的内存。在会话中,占位符可以使用feed_dict馈送数据。
feed_dict是一个字典,在字典中需要给出每一个用到的占位符的取值。在训练神经网络时需要每次提供一个批量的训练样本,如果每次迭代选取的数据要通过常量表示,那么TensorFlow的计算图会非常大。因为每增加一个常量,TensorFlow都会在计算图中增加一个结点。所以说拥有几百万次迭代的神经网络会拥有极其庞大的计算图,而占位符却可以解决这一点,它只会拥有占位符这一个结点。

3.张量
在TensorFlow中,张量是计算图执行运算的基本载体,我们需要计算的数据都以张量的形式储存或声明。如下所示,该教程给出了各阶张量的意义。

零阶张量就是我们熟悉的标量数字,它仅仅只表达了量的大小或性质而没有其它的描述。一阶张量即我们熟悉的向量,它不仅表达了线段量的大小,同时还表达了方向。一般来说二维向量可以表示平面中线段的量和方向,三维向量和表示空间中线段的量和方向。二阶张量即矩阵,我们可以看作是填满数字的一个表格,矩阵运算即一个表格和另外一个表格进行运算。当然理论上我们可以产生任意阶的张量,但在实际的机器学习算法运算中,我们使用得最多的还是一阶张量(向量)和二阶张量(矩阵)。
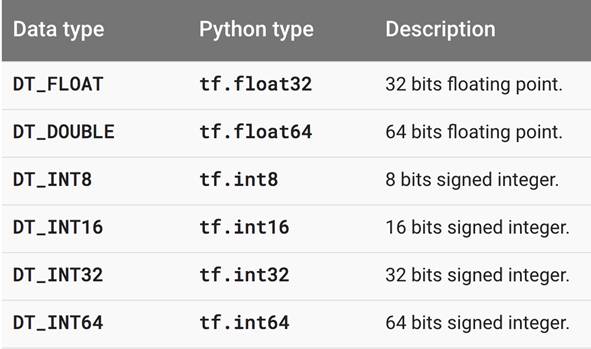
一般来说,张量中每个元素的数据类型有以上几种,即浮点型和整数型,一般在神经网络中比较常用的是32位浮点型。
4.TensorFlow机器
在整个教程中,下面一张示意图将反复出现,这基本上是所有TensorFlow机器学习模型所遵循的构建流程,即构建计算图、馈送输入张量、更新权重并返回输出值。

在第一步使用TensorFlow构建计算图中,我们需要构建整个模型的架构。例如在神经网络模型中,我们需要从输入层开始构建整个神经网络的架构,包括隐藏层的数量、每一层神经元的数量、层级之间连接的情况与权重、整个网络每个神经元使用的激活函数等内容。此外,我们还需要配置整个训练、验证与测试的过程。例如在神经网络中,定义整个正向传播的过程与参数并设定学习率、正则化率和批量大小等各类训练超参数。第二步需要将训练数据或测试数据等馈送到模型中,TensorFlow在这一步中一般需要打开一个会话(Session)来执行参数初始化和馈送数据等任务。例如在计算机视觉中,我们需要随机初始化整个模型参数数值,并将图像成批(图像数等于批量大小)地馈送到定义好的卷积神经网络中。第三步即更新权重并获取返回值,这个一般是控制训练过程与获得最终的预测结果。
TensorFlow模型实战
TensorFlow线性回归
该教程前面介绍了很多线性回归的基本概念,包括直线拟合、损失函数、梯度下降等基础内容。我们一直认为线性回归是理解机器学习最好的入门模型,因为他的原理和概念十分简单,但又基本涉及到了机器学习的各个过程。总的来说,线性回归模型可以用下图概括:
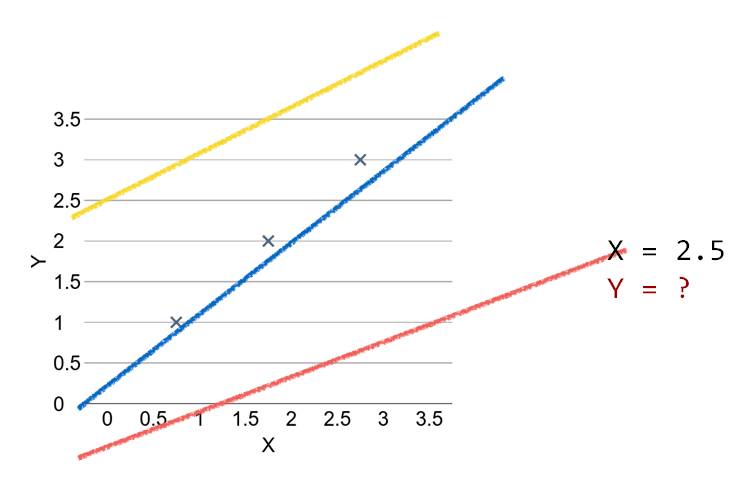
其中「×」为数据点,我们需要找到一条直线以最好地拟合这些数据点。该直线和这些数据点之间的距离即损失函数,所以我们希望找到一条能令损失函数最小的直线。以下是使用TensorFlow构建线性回归的简单案例。
1.构建目标函数(即「直线」)
目标函数即H(x)=Wx+b,其中x为特征向量、W为特征向量中每个元素对应的权重、b为偏置项。
# X and Y data
x_train = [1, 2, 3]
y_train = [1, 2, 3]
W = tf.Variable(tf.random_normal([1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
# Our hypothesis XW+b
hypothesis = x_train * W + b
如上所示,我们定义了y=wx+b的运算,即我们需要拟合的一条直线。
2.构建损失函数
下面我们需要构建整个模型的损失函数,即各数据点到该直线的距离,这里我们构建的损失函数为均方误差函数:
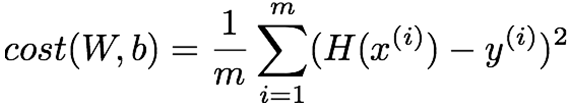
该函数表明根据数据点预测的值和该数据点真实值之间的距离,我们可以使用以下代码实现:
# cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - y_train))
其中tf.square()为取某个数的平方,而tf.reduce_mean()为取均值。
3.采用梯度下降更新权重
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(cost)
为了寻找能拟合数据的最好直线,我们需要最小化损失函数,即数据与直线之间的距离,因此我们可以采用梯度下降算法:
4.运行计算图执行训练
# Launch the graph in a session.
sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
# Fit the line
for step in range(2001):
sess.run(train)
if step % 20 == 0:
print(step, sess.run(cost), sess.run(W), sess.run(b))
上面的代码打开了一个会话并执行变量初始化和馈送数据。
最后,该课程给出了完整的实现代码,刚入门的读者可以尝试实现这一简单的线性回归模型:
import tensorflow as tf
W = tf.Variable(tf.random_normal([1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
X = tf.placeholder(tf.float32, shape=[None])
Y = tf.placeholder(tf.float32, shape=[None])
# Our hypothesis XW+b
hypothesis = X * W + b
# cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(cost)
# Launch the graph in a session.
sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
# Fit the line
for step in range(2001):
cost_val, W_val, b_val, _ = sess.run([cost, W, b, train],
feed_dict={X: [1, 2, 3], Y: [1, 2, 3]})
if step % 20 == 0:
print(step, cost_val, W_val, b_val)
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: lzxmw777