恰逢清明假期,首先表达一下对本次新冠疫情中牺牲医务工作人员的悼念。医生和老师,一个救人一个育人,可以说是当今社会最重要的两个职业,但总觉得没有得到应有的、体面的尊重和待遇。希望这次新冠疫情后,全社会能够尊重医生和老师这两个职业,适度提高这两个职业的福利待遇,peace。

今天想聊一聊资产配置。大家都知道,传统战略资产配置(SAA)寻求建立一个在各种经济环境、市场状态下都表现优异的“全天候”组合,例如过去几年风靡全球的风险平价模型。然而市场状态的转换(尤其近几年)对这种基于历史静态数据的方法提出了重大挑战,典型如桥水的风险平价策略组合,前段时间一度传出因基金亏损遭遇大金主巨额赎回导致流动性危机,虽然时候达里奥出面说明并无组合爆仓但披露的数据显示公司产品今年业绩确实不太好,几个全天候策略组合亏损达10%+

为什么会这样?因为进行资产配置时需要对资产收益风险以及资产收益间的相关性进行预测,作为输入并据此优化出最优的配置比例。但是金融资产特别是高波动资产的收益风险特征往往是不稳定的,表现出随时间迁移而发生变化的特征,静态线性模型在刻画与预测金融资产的收益风险方面存在很大不确定性。
因此,为了准确刻画金融资产收益乃至预测其变化,大量学术文献、卖方报告提出了基于主观经济周期划分的动态资产配置方法,比如货币+信用周期、经济增长+通胀周期、库存周期等等。其中最著名的就是美林时钟,其根据经济通胀指标来判断市场所处状态,并给出对应资产的配置权重。
另一方面,过去十几年金融领域的研究者也提出了大量的动态、时变、非线性的模型与方法,其中一种得到广泛应用的隐马尔可夫机制转换模型,该方法最早由Hamilton(1989)研究美国经济波动时提出,他发现金融数据往往具有“机制转换”特征即在不同时间段内表现出截然不同的分布特征,如宏观经济指标能较为明显地区分为增长和衰退、股票收益能够较为明显地区分为牛市与熊市等等。此后国内外学者又进一步将机制转换模型应用于资产配置,从而形成了基于机制转换的资产配置模型(Regime-Based Asset Allocation)。
上述两种方法都可以较好的捕捉到资产在不同状态下的的不同风险收益特征。但前者主观性、随意性太强,而且往往事后划分拐点容易但当下判断较难。后者通过纯统计方式挖掘资产内在风险收益规律,人为干预少但又可能存在数据挖掘。
理论上讲将两种方法结合起来效果会更佳,目前主观划分方法市场上介绍文献很多很多,本文重点介绍后一种比较新颖的方法,即Regime-Based Asset Allocation(下文简称RBAA)
什么是隐马尔科夫模型?
为了更好的理解RBAA的原理,有必要先简单介绍一下隐马尔科夫模型。本部分较为枯燥无聊,不感兴趣朋友可以直接调到后面的海外应用举例。
隐马尔可夫模型包含了两个随机序列:一个是无法观察到的状态序列(隐藏序列)、一个是可以观察到的观测序列,且可观测变量的概率分布依赖于隐含的状态变量。举个例子:经济状态复苏、滞胀、衰退、萧条是观察不到的,但经济指标如GDP、通胀是观察得到的,且经济指标的分布依然于所处的经济状态。
一个隐马尔可夫模型由初始状态概率分布π、概率转移矩阵A以及观测概率分布B确定。其中初始状态概率分布π决定了初始时刻各个状态的概率,概率转移矩阵A决定了从一个转移到下一个状态的概率;观测概率分布B决定了某个状态下,观测变量的概率分布。模型有两个很强的假设:
1、当前时刻状态只取决于上一时刻状态,即(这里引用了李航《统计学系方法中的公式,i代表状态变量o代表观测变量》):
2、当前观测变量的概率分布只依赖于当前状态,即:
这里以一个两状态(X属于状态1或2)、单观测变量Y的隐马尔科夫模型为例,其转移概率矩阵、观测分布如下:

其对应的从时间0~T的完整隐马尔科夫过程如下:
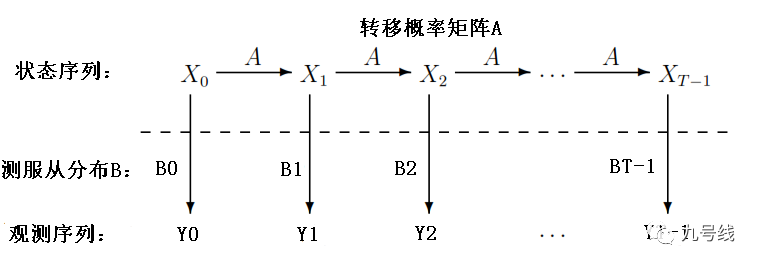
当然实际运用中,状态可以有多个情况(如典型的美林时钟模型4种经济状态),观察序列Y可以是一个多元序列,其服从的分布也可以是多元概率分布。
介绍到这,就引出了隐马尔科夫模型的三个基本问题:
1、概率计算问题,给定初始状态概率分布π、概率转移矩阵A以及观测概率分布B,确定某观察到的序列Yt出现的概率(当然既然已经观测到序列出现,那概率就应该很大);
2、学习问题,给定观察序列Yt,估计模型参数π、A、B,使得该参数条件下观测概率P(Yt|π、A、B)最大,即运用最大使然函数求解参数π、A、B;
3、预测问题,给定模型参数π、A、B和观测序列Yt,使得该参数条件下概率P(Xt|Yt,π、A、B)最大的状态序列Xt,也就是求最有可能的状态序列。
上述三个问题的求解分别对应了前向后向算法(forward、backward)、Baum-Welch算法(其实就是EM算法,一种估计含有隐变量参数的算法)以及Viterbi算法,感兴趣的朋友可以参考李航《统计学习方法》第十章,有详细的数学推导过程,不过书中对应的单观测、离散变量的情况。如果观测是连续变量的情况,易方达王建军博士《Markov机制转换模型研究及其在经济周期分析中的应用》一文中不仅考虑了实际观测变量的连续性而且考虑了大多数经济变量的持续性,更符合实际的金融经济数据情况。
该文以带有一阶滞后项、基于两状态条件正态分布的马尔科夫机制转换模型为例,推导出了对应的最大似然函数,整个过程简单总结如下,有兴趣的朋友可参考原文:

一般初始状态ε1|0也就是前文提到的初始状态概率分布π,可以设为等权重,即初始每个状态出现概率相等。最后将所用样本数据带入模型的对数似然函数(2.2.26),再运用EM算法求Q函数并对其求最大值,最终收敛得到使得对数似然函数取得最大值的各参数估计值。
回到本文主题基于机制转换的资产配置模型,下面介绍几个海外应用隐马尔科夫模型进行动态资产配置的例子。实际运用中,状态的确定有两个思路:第一个思路是根据经济指标划分不同的状态,然后根据不同状态下资产风险收益的不同分布进行资产配置;第二个思路是认为组合的风险收益特征主要取决于风险资产(比如权益),所以直接根据风险资产的收益率进行市场状态划分,比如根据标普500指数收益率将市场划分为常规市场和非常规市场,然后作相应的资产配置,下面分别通过三个例子介绍这两种应用。
1、基于宏观经济状态划分的RBAA
Kritzman等人在《Regime Shifts: Implications for Dynamic Strategies》一文中,从金融市场动荡(Financial Market Turbulence)、经济增长(Economic Growth. We)、通货膨胀(Inflation)三个维度来划分状态。其中:
金融市场骚动又分为股票市场动荡和货币市场动荡两个细分纬度,股票市场根据10个标普500行业指数收益率的马氏距离(Mahalanobis distance)来衡量股票市场动荡,货币市场则根据G10集团货币相对美元收益率的马氏距离(Mahalanobis distance)来衡量货币市场动荡。股票市场数据采用过去10年的日度数据滚动计算,货币市场数据采用过去3年的日度数据滚动计算,最后求月平均得到两个序列的月度数据。

通胀方面,采用季调后的U.S. Consumer Price Index for All Urban Consumers求月度变化率。经济方面,采用美国季调后的真实GNP的季度变化率。
作者假设这四个指标服从正态分布,并用隐马尔科夫模型2状态(正常状态normal regime和非常规状态event regime)模型分析这四个经济指标序列,对其进行状态划分并发现四个指标在两个状态下的均值、方差存在显著差异:
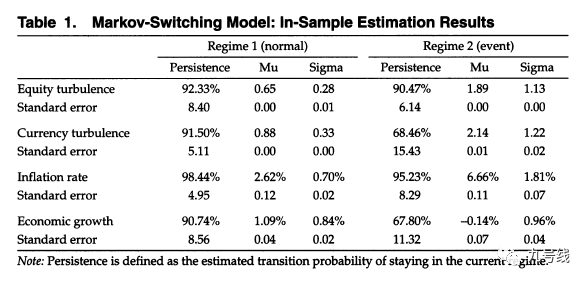
作者首先验证了基于机制转换的动态因子配置模型,定义了如下几个风险因子,例如受股票市场动荡影响的Gloab stocks-bond、Equity momentum风险因子,受货币动荡影响的FX carry strategy、FX valuation strategy风险因子等等。
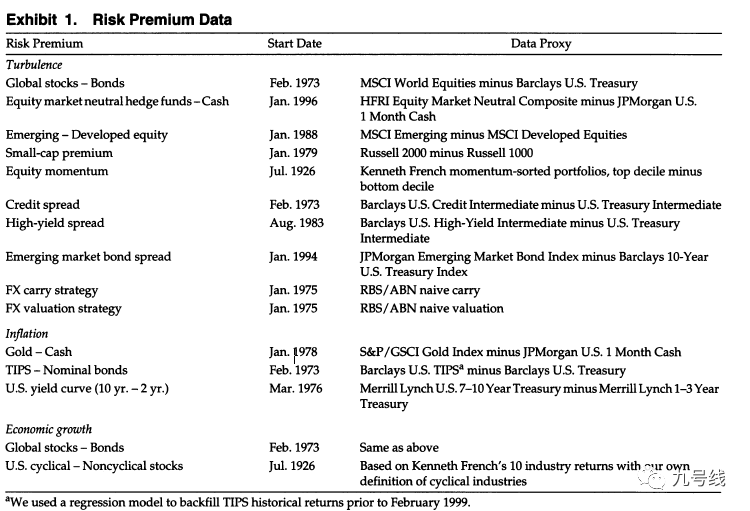
根据样本内统计,作者发现上述风险因子在event regime下的平均收益率与normal regime下的平均收益率存在显著差异(两者之差/全样本波动率进行标准化)。例如在权益处于动荡状态时,Gloab stocks-bond因子收益率比权益处于正常状态时低2个标准差;当通胀处于动荡状态时,U.S. yield curve (10yr-2yr)因子收益率比通胀处于正常状态时低1.13个标准差;当经济处于动荡状态时,U.S. cyclical – Noncyclical stocks因子收益率比经济处于正常状态时低1.31个标准差。由此验证了处于不同权益、通胀、经济状态时,构造的风险因子有显著不同的收益率。
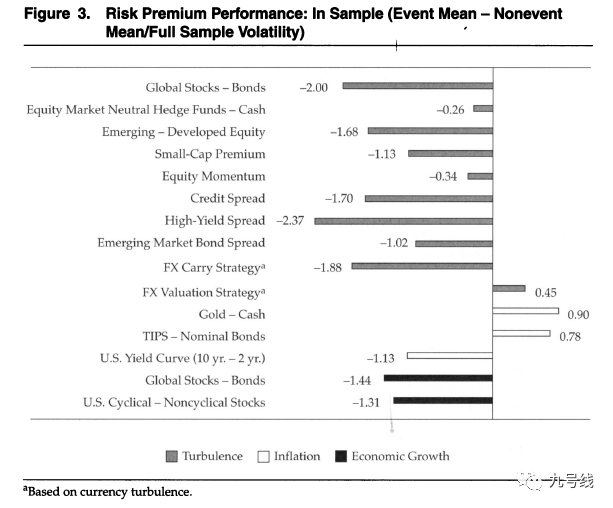
为了验证动态因子配置的有效应,作者构建了两个组合:一个是静态等权风险因子组合(基准组合)、一个根据上述四个指标的状态构建的动态风险因子组合,动态调整方法如下:
1、每个月初,对4个指标运用固定窗口模型(如前所示,指标的计算是滚动窗口的),计算其从开始到当月的状态序列,并求当时概率最大的状态(normal or event);
2、根据得到的状态,对静态组合进行调整。调整方法如下表。举例来说,如果当月权益处于动荡状态时,减少5%Gloab stocks-bond因子的配置比例;如果当月通胀处于动荡状态时,增加10%Gold – Cash和TIPS – Nominal bonds因子的配置比例,以此类推。
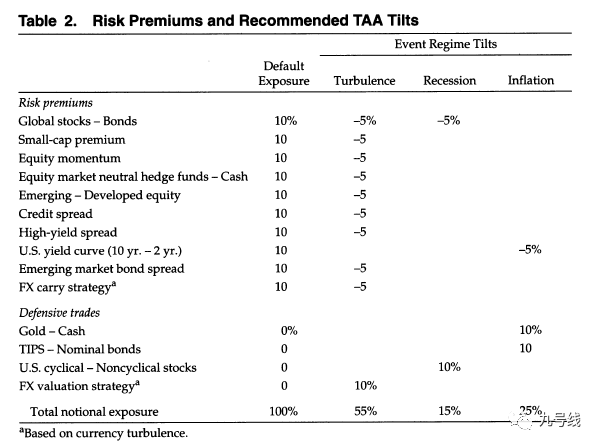
最后将动态因子配置组合和静态因子配置组合比较如下,可以看到动态因子配置组合的各项指标均显著好于等权静态因子配置组合。
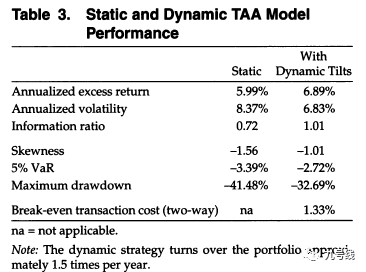
接着作者在大类资产上进行了类似的实证分析,采用如下大类资产指数以及月度动态调整方法,同样得到了基于机制转换的动态资产配置模型要好于静态资产配置模型的结论,不再赘述。

2、基于资产收益率划分的RBAA
再来看一看直接根据风险资产收益率(比如股票指数)划分状态并进行动态资产配置的效果如何。
与前一个例子不同,PETER NYSTRUP等人在《Dynamic Allocation orDiversification: A Regime-BasedApproach to Multiple Assets》一文中,直接根据MSCI World Index的日度对数收益率来划分市场状态。理由一是组合风险主要来自股票资产,理由二是股票收益率通常领先经济。接着利用HMM模型将市场状态划分为高波动状态和低波动状态,并认为高波动意味着低风险回报而低波动意味着高风险回报,并据此进行动态资产配置。
作者用到的资产类别包括发达市场股票、新兴市场股票、房地产、发达市场及新兴市场高收益债券、黄金、原油、公司债券、通胀调整债券以及政府债券等,所有指数收益率以美元计价净回报衡量。
为了比较动态资产配置的效果,作者首先构建了传统的60/40组合,即60%高风险资产、50%低风险资产(因为跟权益市场相关性更大,因此本文将高收益债归为高风险资产)。接着设定了一个组合调节参数p,表示最终组合有多少比例分配给动态资产配置,以及剩余有多少分配给基准组合。例如p=0.5时表示最终组合配置中的50%由RBAA策略确定,剩下的50%由基准60/40组合构成。
Risk-on和Risk-off组合分别表示在低波动和高波动状态下的RBAA配置组合。在低波动状态下应该Risk-on,因此组合中与股票相关性高的资产比例提高到80%,而固定收益类资产的比例降低到了只有20%。高波动状态下的Risk-off则相反。
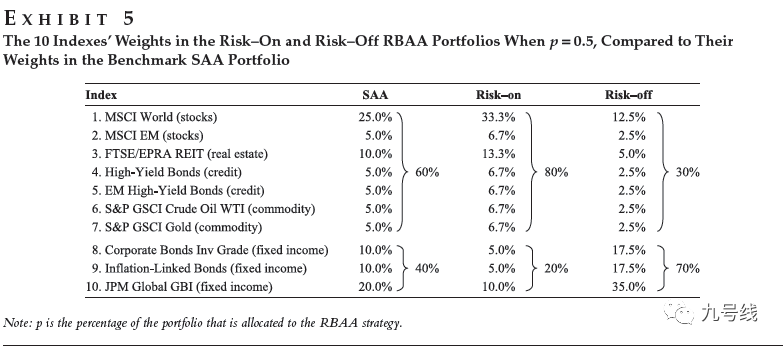
这里有个小技巧,作者推测当前处于什么状态时并没有用传统的Viterbi方法,而是用了在线Viterbi方法(我理解就是固定起点的扩展窗口)并设定了一个阈值来判断当前状态。由于设定了阈值,因此状态的判断不仅仅取决于概率,而是当属于某状态的概率超过该阈值时才更新为该状态否则保留之前状态。这个阈值的选择也有讲究,等于1-1/T≈ 0.9998,这里T是观测序列的长度。
下一步就是组合构建,首先预留出一个长度为t的观测序列(MSCI World Index日度对数收益率)学习模型参数并计算t日所属状态,然后根据概率是否大于阈值预测t+1日所属状态,若不改变则保留原组合的资产配置,若改变则在t+1日收盘后更新组合资产配置。最后将学习序列扩展为t+1并重新学习模型参数,上述过程从1998.1.1日起开始重复,最终得到结果如下。可以看到,在市场高波动状下RBAA(p=0.5)组合的回撤控制得较好。
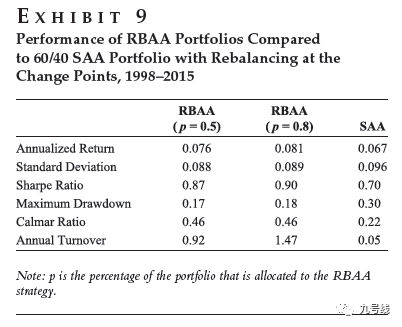
值得注意的是,参数p的选择对RBAA组合的收益风险特征影响很大,为此作者进行了多种尝试,最后在p=0.8时组合的夏普比最高。看来该组合构建方法对参数p的敏感性还是很大的。

3、基于资产收益率划分的RBAA(概率加权求资产权重)
最后再来看一篇同样基于资产收益率划分状态并进行动态大类资产的文献:王霞、魏先华的《资产收益的区制转换特征与动态大类资产配置》。该文覆盖的资产类别包含债券、股票、黄金三类,分别使用巴克莱美国综合债券指数(BarclaysCapital US Aggregate Bond Index)、标普500 指数与伦敦现货黄金价格代表。
虽然同样根据资产收益率将状态划分为高波动(机制1)和低波动(机制2),但本文最大的创新在于:根据不同状态下资产收益率不同的均值、方差、协方差分布,求最终的加权优化权重:
简单说就是当未来风险资产处于状态1时(同样的,本文认为状态主要由风险资产决定),根据风险资产、低风险资产的均值、方差及协方差矩阵计算得到一个资产配置比例;当未来风险资产处于状态2时,根据风险资产、低风险资产的均值、方差及协方差矩阵计算又得到一个新的资产配置比例,根据状态1、2的预测概率将两者进行加权平均得到最终的资产配置比例。
这么做是合理的。马尔可夫转换模型基于对历史数据的计算估算当前状态,当资产处于两种机制转换的临界点或噪声较大数据表现不稳定时,模型可能无法对资产所处的区制给出较明确的判断,比如判断当前状态为1的概率是45%,为状态2的概率是55%。因此在使用状态概率值对配置权重进行加权处理,这样当资产所处机制不明确时,最终的配置权重将是一个较为中庸的结果,在一定程度上规避了出现较大投资失误的可能性。
实证检验中作者用到了传统的均值方差模型和风险平价模型,每月初使用过去240 个月(是的原文此处为240个月即过去10年)的月度资产收益率数据估计模型参数,得到资产的均值、方差及协方差矩阵,并预测最新一期的状态输入上述两个模型后得到权重。
基准组合A与基准组合B分别是上述组合的基准组合,在参数估计中没有使用区制转换模型而是直接使用历史数据估算预期收益与方差-协方差矩阵并计算配置权重。
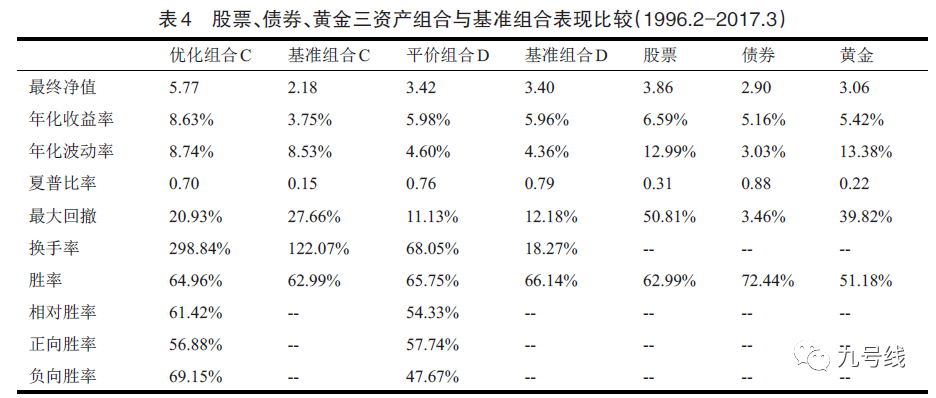
首先是只包含股债两类资产的组合,应用机制转换模型的优化组合A与平价组合B在收益、风险以及综合表现都要优于其对应的基准组合。
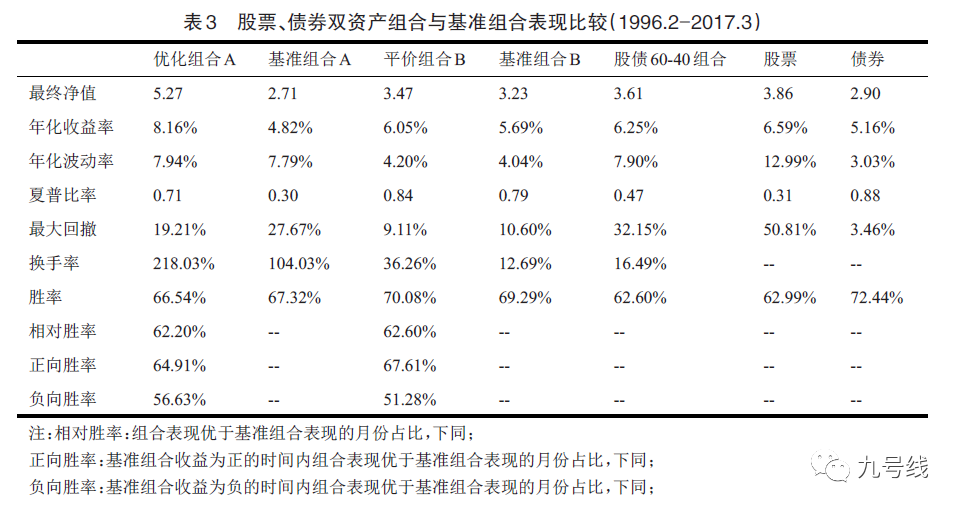
接着加入黄金资产,应用机制转换模型的优化组合C与其基准组合C相比在收益与风险表现上都有较好的改善。但平价组合D与基准组合D相比并没有明显的改善,并且在年化波动率与夏普比率上反而劣于基准组合。
作者认为黄金资产在高波动状态下收益更高而在低波动状态下收益较低,且通过计算发现黄金资产在高波动状态的夏普比率(0.89)也高于低波动状态的夏普比率(-0.06),因此使用风险平价方法进行配置时,当黄金处于高波动状态时风险平价方法给予其较小的权重,而此时黄金的收益与夏普比率是较高的;当黄金处于低波动状态时给予其较高的权重,但此时黄金收益与夏普比率较低,由此成平价组合D的表现劣于基准组合D。
这个结论其实符合目标波动率领域的研究结果,波动率控制主要控制高波动低收益的资产而不是高波动高收益的资产。
因此,作者重新构建了优化组合E与平价组合F,在这两个组合中只对股票资产应用机制转换模型,而债券和黄金不考虑。相应的基准组合仍为基准组合C与基准组合D。
下表可以看到,平价组合F的表现要优于基准组合D,这和平价组合D形成对比,说明在风险平价组合中忽略黄金的机制转换特征有助于提高组合的表现。与此形成对比的是,优化组合E同样忽略了黄金的机制转换特征,但其年化收益与考虑了黄金收益机制转换特征的优化组合C相比有所下降。
为什么会这样?主要跟风险平价的权重配比机制有关。当资产收益表现出机制转换特征时,若不同机制间波动率与夏普比率表现出正相关(如黄金),风险平价更倾向于在资产综合表现较差时给予其较大权重(即低波低夏普时给予较大权重),从而使得资产组合表现较差;而当资产收益不同机制间的波动与夏普比率负相关(如股票)时,风险平价更倾向于在资产综合表现较优时给予其较大权重(低波动高夏普时给予较大权重),从而提升资产组合的表现。因此在风险平价组合中,忽略黄金资产的机制转换特征反而能够提升组合的表现。而在均值-方差优化方法中,忽略资产的机制转换特征会对资产组合的收益产生不利影响。
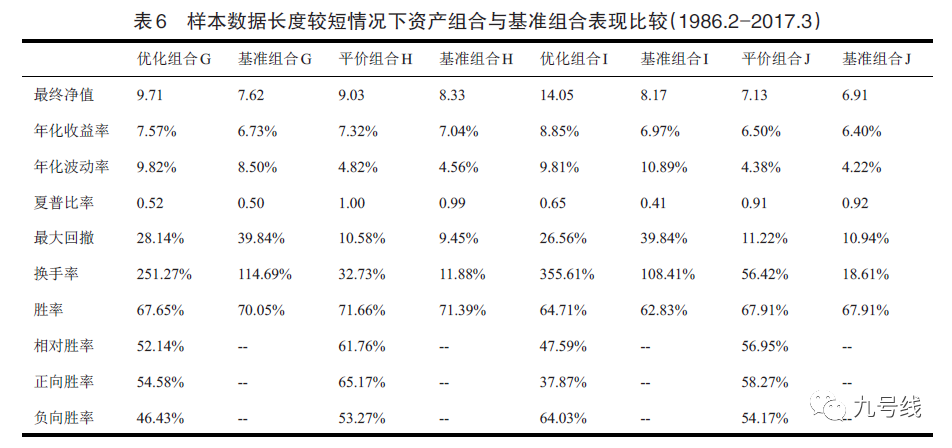
最后作者进行了几个稳定性检验,比如将学习模型参数用到的回测区间由240个月减少为120个月,结果显示在使用更短历史数据估计模型参数的情况下,应用机制转换模型的配置策略仍然要优于相应的基准配置组合,特别是优化组合I在各项指标上都较其基准组合I更优(这里G和H仅考虑股、债两资产,I和J考虑了股、债、黄金三资产)。
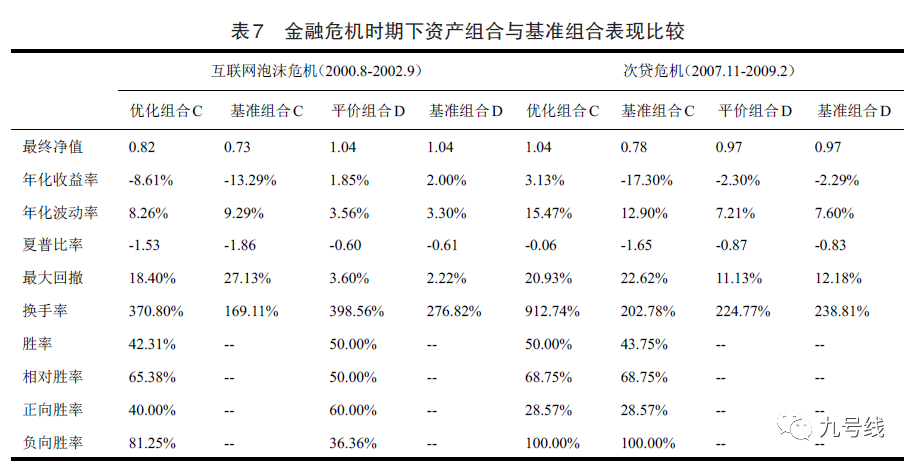
再比如金融危机期间的表现,主要是互联网泡沫时期和金融危机时期。下表结果表明,在两次金融危机期间优化组合C的表现要明显优于基准组合C,特别是在2008 年次贷危机中,优化组合C在市场整体下跌的情况下实现了正的收益;而平价组合D与基准组合D在两次危机期间的表现没有明显差异。
好了,关于基于机制转换的资产配置的原理和海外应用就介绍到这里,下一篇我将针对国内常见的大类资产,运用基于机制转换的动态资产配置模型进行实证应用,同时详细介绍一个R语言环境下做HMM分析的功能强大的包
。
这里可以先推荐一本经典的HMM教材给大家,人大BBS上有下载:

四、参考文献
1、王建军,《Markov机制转换模型研究及其在经济周期分析中的应用》
2、李航,《统计学习方法》
3、Hamilton,《A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle》
4、Mark Kritzman, Sébastien Page and David Turkington,《Regime Shifts: Implications for Dynamic Strategies》
5、PETER NYSTRUP, BO WILLIAM HANSEN, HENRIK OLEJASZ,《Dynamic Allocation orDiversification: A Regime-BasedApproach to Multiple Assets》
6、王霞、魏先华,《资产收益的区制转换特征与动态大类资产配置》






